Плавание тел
Условия плавания тел
Условия плавания тел следуют из закона Архимеда:
- Если выталкивающая сила больше, чем вес тела
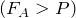 , тело всплывает до тех пор, пока эти силы не уравновесятся.
, тело всплывает до тех пор, пока эти силы не уравновесятся. - Если выталкивающая сила равна весу тела
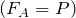 , тело плавает в любой точке жидкости.
, тело плавает в любой точке жидкости. - Если выталкивающая сила меньше веса тела
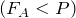 , тело тонет.
, тело тонет.
Глубина погружения плавающего тела зависит от соотношения плотностей тела и жидкости. Если учесть, что ![]() и
и ![]() , то тело будет плавать в жидкости, если
, то тело будет плавать в жидкости, если ![]() (здесь
(здесь ![]() и
и ![]() — плотность и объем тела,
— плотность и объем тела, ![]() — плотность жидкости, а
— плотность жидкости, а ![]() — объем погруженной части тела).
— объем погруженной части тела).
Из полученного соотношения можно сделать важные выводы:
- тело плавает, будучи полностью погруженным в жидкость, если плотность тела равна плотности жидкости:
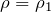 ;
; - тело плавает, частично выступая над поверхностью жидкости, если плотность тела меньше плотности жидкости:
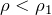 ;
; - если плотность тела больше плотности жидкости, т.е
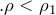 , плавание невозможно.
, плавание невозможно.
Плавания тел на границе нескольких сред
Если тело плавает на границе нескольких сред с плотностями ![]() то вес вытесненной жидкости, а, следовательно, и Архимедова сила в этом случае равны:
то вес вытесненной жидкости, а, следовательно, и Архимедова сила в этом случае равны:
![]()
где ![]() — объем части тела, погруженной в первую среду,
— объем части тела, погруженной в первую среду, ![]() — объем части тела, погруженной во вторую среду и т.д.
— объем части тела, погруженной во вторую среду и т.д.
Плотность сухого дерева за счет полостей, наполненных воздухом, меньше плотности воды, и дерево может плавать на поверхности. Но железо и многие другие вещества значительно плотнее воды. Однако современные корабли сделаны из металла и перевозят различные грузы по воде. Как это возможно? Дело в том, что корпус корабля, который погружается в воду, делают объемным, а внутри этот корабль имеет большие полости, заполненные воздухом, что и уменьшает общую плотность корабля.
Глубина, на которую плавающий корабль погружается в воду, называется осадкой корабля. При полной загрузке корабль не должен опускаться ниже так называемой грузовой ватерлинии. Вес воды, вытесняемой судном при погружении до ватерлинии, называется водоизмещением судна. Он равен силе тяжести, действующей на судно с грузом. Грузоподъемность судна показывает вес груза, который перевозится судном. Грузоподъемность равна разности водоизмещения и веса незагруженного судна.
Плотность человеческого тела немного больше плотности воды. Однако, человек, когда у него в легких содержится некоторое количество воздуха, тоже может спокойно держаться на поверхности воды. Если же, находясь в воде, выдохнуть весь воздух из легких, то начнется медленное погружение на дно. Поэтому при плавании опасно наглотаться воды и впустить ее в легкие, именно это является наиболее частой причиной несчастных случаев на воде.
Примеры решения задач
| Задание | Льдина, имеющая форму призмы, плавает в воде, высовываясь наружу на 2 см. Какова масса льдины, если площадь ее основания равна 2000 см |
| Решение | Так как льдина плавает в воде, должно выполняться условие:
или Объем погруженной части льдины: где Подставив выражение для объема погруженной части льдины в условие плавание, получим: откуда объем всей льдины: Учитывая, что имеем: откуда масса льдины: Переведем единицы в систему СИ. Высота выступающей части льдины Плотность воды (из таблиц) Вычислим: |
| Ответ | Масса льдины 46 кг. |
| Задание | Деревянный цилиндр плавает в воде так, что |
| Решение | Выполним рисунок.
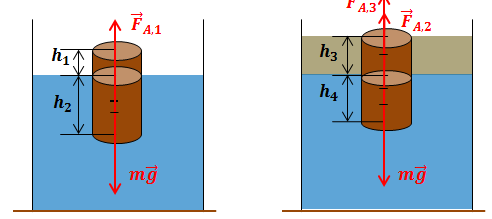
В первом случае на цилиндр действуют сила тяжести Во втором случае на цилиндр действуют сила тяжести Обозначим Подставив эти соотношения в условия равновесия и сократив на Из первого уравнения системы определяем плотность дерева: Так как по условию задачи: имеем Второе уравнение системы разделим на Так как откуда часть цилиндра, погруженная в воду во втором случае: или с учетом выражения для плотности дерева: Из таблиц плотность воды Вычислим: |
| Ответ | Если на воду налить слой масла, полностью закрывающий цилиндр, в воду будет погружена половина цилиндра. |











