Вес тела. Невесомость и перегрузка
Вес ![]() , как и любая другая сила, в системе СИ измеряется в Ньютонах.
, как и любая другая сила, в системе СИ измеряется в Ньютонах.
Следы на снегу или на песке свидетельствуют о том, что человек или животное, проходя, давит на снежную или песчаную опору с некоторой силой.
Вес тела во время движения. Состояния невесомости и перегрузки
Вес тела зависит от ускорения, с которым движется тело, а потому может быть различным:
- Если тело покоится или движется равномерно прямолинейно, т.е. ускорение тела равно нулю, вес тела равен силе тяжести.
![Rendered by QuickLaTeX.com \[\overline{N}+m\overline{g}=0\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-5fd396c6c99a84924a0c7e31751ac6b3_l3.png)
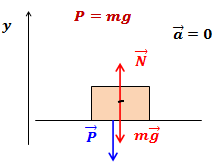
или в проекции на ось
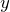 :
:![Rendered by QuickLaTeX.com \[N-mg=0\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-3e0e298de2dc284063fdebb3fb39fe97_l3.png)
откуда
![Rendered by QuickLaTeX.com \[N=mg\ \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ed721a55e9eb9962599ca41a3ef1c38f_l3.png)
![Rendered by QuickLaTeX.com \[\left|\overline{P}\right|=\left|\overline{N}\right|=mg\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-4ed2ab0bf30c13cf1f3dd3e4643386d4_l3.png)
- Если тело движется с ускорением, направленным вертикально вверх, вес тела увеличивается. Такое состояние тела называется перегрузкой.
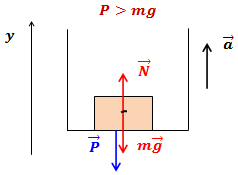
По второму закону Ньютона:
![Rendered by QuickLaTeX.com \[\overline{N}+m\overline{g}=m\overline{a}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-06aef95dce4348baf4ccb1c33598cb64_l3.png)
или в проекции на ось
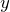 :
:![Rendered by QuickLaTeX.com \[N-mg=ma\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-6c1bd7b7fabe0984e027dfe512baf67a_l3.png)
откуда
![Rendered by QuickLaTeX.com \[N=m(g+a)\ \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-14eef652bb2ca91aacb243ad6a57dd50_l3.png)
По третьему закону Ньютона:
![Rendered by QuickLaTeX.com \[\left|\overline{P}\right|=\left|\overline{N}\right|=m(g+a)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-47e4d5db19a023f9a4fdea5d84c119a4_l3.png)
Перегрузки испытывают космонавты при взлете и на участках торможения космического корабля, летчики при выполнении фигур высшего пилотажа, пассажиры лифта при разгоне или торможении лифта и т.д.
- Если тело движется с ускорением, направленным вертикально вниз, вес тела уменьшается.
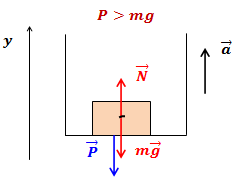
По второму закону Ньютона:
![Rendered by QuickLaTeX.com \[\overline{N}+m\overline{g}=m\overline{a}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-06aef95dce4348baf4ccb1c33598cb64_l3.png)
или в проекции на ось
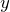 :
:![Rendered by QuickLaTeX.com \[N-mg=-ma\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-74df0bc3da0758eb2d81e90324317b6a_l3.png)
откуда
![Rendered by QuickLaTeX.com \[N=m(g-a)\ \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-7378ca655a740184643f3286536a72d9_l3.png)
По третьему закону Ньютона:
![Rendered by QuickLaTeX.com \[\left|\overline{P}\right|=\left|\overline{N}\right|=m(g-a)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-a01eacc0bb6e6e5c567bf8d975cc5ba8_l3.png)
Если ускорение тела в этом случае будет равно ускорению свободного падения, вес тела равен нулю, т.е. тело будет находиться в состоянии невесомости.
Поскольку вес покоящегося тела равен силе тяжести, часто считают, что вес и сила тяжести – это одна и та же сила. Однако это неверно. Во-первых, вес и сила тяжести приложены к разным телам: сила тяжести приложена к телу, а вес – к опоре или подвесу. Во-вторых, вес и сила тяжести имеют различную физическую природу: вес, как правило, является силой упругости, а сила тяжести – это сила гравитационного взаимодействия. Наконец, как было показано выше, вес тела изменяется с изменением ускорения и может быть равен нулю, когда сила тяжести нулю не равна.
Примеры решения задач
| Задание | При раскрытии парашюта скорость парашютиста уменьшается с 50 до 10 м/с за 1 с. Какую перегрузку испытывает парашютист? |
| Решение | Сделаем рисунок.
На парашютиста действуют сила тяжести По второму закону Ньютона: или в проекции на ось откуда сила натяжения строп парашюта: По третьему закону Ньютона: Ускорение парашютиста при раскрытии парашюта: поэтому вес парашютиста: Вычислив: имеем: |
| Ответ | Парашютист испытывает перегрузку |
| Задание | Сколько оборотов в сутки должна была бы совершать Земля, чтобы на экваторе вес тела обратился в нуль? |
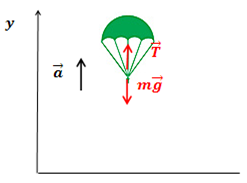
| Решение | На тело, которое находится на экваторе планеты, действует гравитационная сила 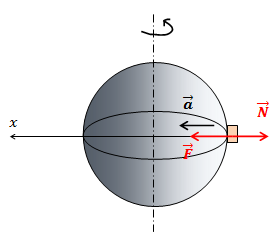
или в проекции на ось откуда По условию задачи тело на экваторе должно находиться в состоянии невесомости, т.е. поэтому можно записать: или По закону всемирного тяготения, гравитационная сила: Центростремительное ускорение: Тогда или откуда скорость тела: Период обращения Земли, т.е. время, за которое Земля делает один полный оборот: Количество оборотов планеты за время Гравитационная постоянная Время Подставив в формулу численные значения физических величин, вычислим: |
| Ответ | Чтобы вес тела на экваторе обратился в нуль, Земля должна делать |






![Rendered by QuickLaTeX.com \[N=\frac{86400}{2\pi \cdot 6,4\cdot {10}^6}\cdot \sqrt{\frac{6,7\cdot {10}^{-11}\cdot 6\cdot {10}^{24}}{6,4\cdot {10}^6}}=1,7\cdot {10}^7\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f2211e78a09cb00081d6d202349ef43c_l3.png)





