Условие равновесия тела

Условие равновесия невращающегося тела

ОПРЕДЕЛЕНИЕ

Тело, не имеющее оси вращения, находится в состоянии равновесия, если геометрическая сумма действующих на него сил равна нулю:

$\sum_i{{\overline{F}}_i}=0$

Это правило можно сформулировать по-другому:

Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы сумма проекций приложенных к нему сил на любую ось была равна нулю:

$\left\{ \begin{array}{c} \sum_i{F_{x,i}=0} \\ \sum_i{F_{y,i}=0} \\ \sum_i{F_{z,i}=0} \end{array} \right.\ \$

При вычислении равнодействующей (геометрической суммы сил) все силы приводятся к одной точке.

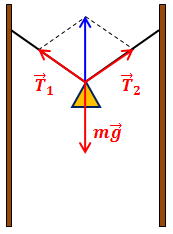
Рис.1. Равновесие тела, не имеющего оси вращения

На рисунке 1 показано тело, подвешенное на тросах к двум опорам. В данном случае равнодействующая сил натяжения первого и второго троса ${\overline{T}}_1$ и ${\overline{T}}_2$ уравновешивается силой тяжести $m\overline{g}$ .

Примеры решения задач

ПРИМЕР 1

Задание

Деревянный брусок лежит на наклонной плоскости. С какой силой нужно прижать брусок к наклонной плоскости, чтобы он оставался на ней в покое? Масса бруска 2 кг, длина наклонной плоскости 1 м, высота 60 см. Коэффициент трения бруска о наклонную плоскость равен 0,4.

Решение

На брусок на наклонной плоскости действуют сила тяжести 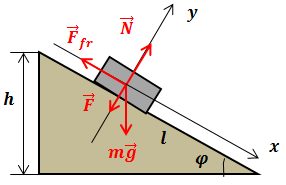$m\overline{g}$ , сила реакции опоры $\overline{N}$ , сила трения ${\overline{F}}_{fr}$ и внешняя сила $\ \overline{F}$ , прижимающая брусок к наклонной плоскости.

Брусок не может вращаться. Поэтому для того, чтобы брусок находился в покое, должно выполняться условие равновесия для тела, не имеющего оси вращения:

$m\overline{g}+\overline{N}+{\overline{F}}_{fr}+\overline{F}=0$

Выбрав направления осей x и y и спроектировав на них условие равновесия, получим:

$\left\{ \begin{array}{c} mg\sin\varphi -F_{fr}=0 \\ N-mg\cos\varphi -F=0\ \end{array} \right$

или

$\left\{ \begin{array}{c} F_{fr}=mg\sin\varphi \\ N-F-mg\cos\varphi =0 \end{array} \right$

Сила трения:

$F_{fr}=\mu N$

поэтому можно записать:

$mg\sin\varphi =\mu N$

откуда сила реакции опоры:

$N=\frac{mg\sin\varphi }{\mu }$

Подставив последнее выражение во второе уравнение системы, найдем внешнюю силу $F:$

$F=\frac{mg\sin\varphi }{\mu }-mg\cos\varphi =mg\left(\frac{\sin\varphi }{\mu }-\cos\varphi \right)$

Из геометрии задачи:

${\sin \varphi =\frac{h}{l};\ \ {\cos \varphi =\frac{\sqrt{h^2-l^2}}{l}\ }\ }$

Поэтому внешняя сила:

$F=\frac{mg}{l}\left(\frac{h}{\mu }-\sqrt{h^2-l^2}\right)$

Переведем высоту наклонной плоскости в систему СИ: $h=60$ см $=0,6$ м

Ускорение свободного падения $g=9,8$ м/с $^{2}$ .

Вычислим:

$F=\frac{2\cdot 9,8}{1}\cdot \left(\frac{0,6}{0,4}-\sqrt{1^2-{0,6}^2}\right)=13,7\ H$

Ответ

К бруску нужно приложить силу 13,7 Н.

ПРИМЕР 2

Задание

Электрическая лампа массой 2 кг подвешена к потолку на шнуре AB, а затем оттянута к стене веревкой BC. Определить натяжение шнура AB и веревки BC, если углы соответственно равны $\alpha ={60}^\circ,\ \beta ={135}^\circ$ .

Решение

Выполним рисунок и укажем силы, действующие на лампу.

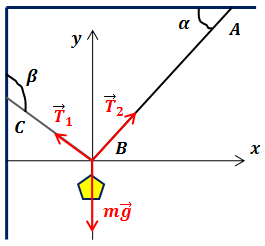
Запишем условие равновесия:

$m\overline{g}+{\overline{T}}_1+{\overline{T}}_2=0\$

Выберем координатные оси, как показано на рисунке, и спроектируем уравнение на направления осей координат:

$\left\{ \begin{array}{c} T_2{\cos \alpha -T_1{\cos \left({90}^\circ-\beta \right)=0\ }\ } \\ T_2{\sin \alpha -T_1{\sin \left({90}^\circ-\beta \right)-mg=0\ \ }\ } \end{array} \right$