Сообщающиеся сосуды
Другими словами, это сосуды, соединенные ниже поверхности жидкости таким образом, что жидкость может перетекать из одного сосуда в другой (рис.1).
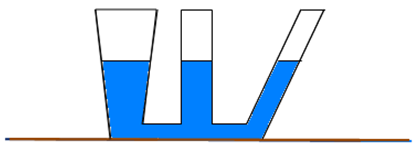
Рис.1. Пример сообщающихся сосудов
Закон сообщающихся сосудов
- В сообщающихся сосудах, заполненных однородной жидкостью, давление во всех точках жидкости, расположенных в одной горизонтальной плоскости, одинаково и не зависит от формы сосудов. При этом поверхности жидкости в сообщающихся сосудах устанавливаются на одном уровне.
- Высоты столбов разнородных жидкостей обратно пропорциональны плотностям этих жидкостей:
![Rendered by QuickLaTeX.com \[\frac{h_1}{h_2}=\frac{{\rho }_2\ }{{\rho }_1}\ \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f9b46c86f219025c690442c334997a92_l3.png)
Сообщающиеся сосуды широко используются в быту и в технике. Самый обычный чайник или лейка для полива растений — это примеры сообщающихся сосудов. Закон сообщающихся сосудов лежит в основе работы водопровода, различных фонтанов, шлюзах на реках и каналах.
Примеры решения задач
| Задание | В сообщающихся сосудах находятся ртуть, вода и керосин. Какова высота слоя керосина, если высота столба воды равна 20 см, и уровень ртути в правом колене ниже, чем в левом, на 0,5 см? |
| Решение | Выполним рисунок.
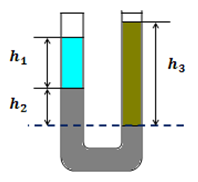
Пусть На уровне или откуда высота столба керосина: По таблицам определим плотности жидкостей: плотность воды плотность ртути плотность керосина Переведем единицы в систему СИ. Высота столба воды Вычислим: |
| Ответ | Высота столба керосина 33,5 см. |
| Задание | В сосуд с водой вставлена трубка сечением 2 см |
| Решение | Выполним рисунок.
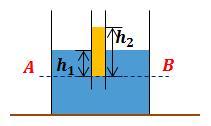
В данном случае трубка и сосуд с водой — сообщающиеся сосуды. Давления жидкостей в обоих сосудах на уровне откуда высота уровня воды: Разность между верхними уровнями масла и воды: Объем масла в цилиндрической трубке: откуда высота столба масла: Учитывая, что объем масла имеем: Подставив последнее соотношение в выражение для разности уровней жидкостей, получим: По таблицам определяем плотности жидкостей: плотность воды плотность масла Переведем единицы в систему СИ. Масса масла Вычислим: |
| Ответ | Разность между верхними уровнями масла и воды 4 см. |











