Тройной интеграл

Понятие тройного интеграла вводиться аналогично понятию двойного интеграла.

Пусть функция $u=f\left( x;\ y;\ z \right)$ определена в ограниченной замкнутой области $\Omega$ , которая принадлежит трехмерному пространству с определенной декартовой системой координат $Oxyz$ . Разобьем заданную область на $n$ частей ${{\Omega }_{i}}$ , которые не имеют общих внутренних точек и объемы которых равны соответственно $\Delta {{V}_{i}},\ i=\overline{1;\ n}$ . В каждой такой элементарной области возьмем произвольную точку ${{P}_{i}}\left( {{x}_{i}};\ {{y}_{i}};\ {{z}_{i}} \right)$ и составим сумму $\sum\limits_{i=1}^{n}{f\left( {{x}_{i}};\ {{y}_{i}};\ {{z}_{i}} \right)\Delta {{V}_{i}}}$ , называемую интегральной суммой для функции $u=f\left( x;\ y;\ z \right)$ по области $\Omega$ .

Пусть $\lambda =\underset{1\le i\le n}{\mathop{\max }}\,d\left( {{\Omega }_{i}} \right)$ – наибольшее из расстояний между точка элементарной области ${{\Omega }_{i}}$ . Если существует предел $\underset{\lambda \to 0}{\mathop{\lim }}\,\sum\limits_{i=1}^{n}{f\left( {{x}_{i}};\ {{y}_{i}};\ {{z}_{i}} \right)\Delta {{V}_{i}}}$ , который не зависит ни от способа разбиения области $\Omega$ на элементарные области ${{\Omega }_{i}}$ , ни от выбора в них точек ${{P}_{i}}$ , то этот предел называется тройным интегралом по области $\Omega$ и обозначается

$\iiint\limits_{\Omega }{f(x;y;z)dV} \text{ }\text{ } , \text{ }\text{ } \iiint\limits_{\Omega }{f(x;y;z)dxdydz}$

Пусть $\Omega$ – замкнутая пространственная область, которая ограничена снизу и сверху поверхностями $z={{\phi }_{1}}\left( x;\ y \right)$ и $z={{\phi }_{2}}\left( x;\ y \right)$ соответственно ( ${{\phi }_{2}}\left( x;\ y \right)\ge {{\phi }_{1}}\left( x;\ y \right)$ ), а з боку – цилиндрической поверхностью с образующими, параллельными оси $Oz$ (рис. 1).

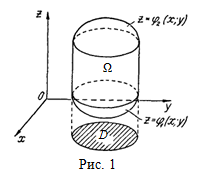
Переменные $x$ и $y$ изменяются в плоской области $D$ , которая является проекцией пространственной области $\Omega$ на координатную плоскость $Oxy$ .

В прямоугольной декартовой системе координат элемент объему $dv$ вычисляется по формуле $dv=dxdydz$ . Для указанной области $\Omega$ тройной интеграл равен:

$\iiint\limits_{\Omega}{f(x; y; z)dxdydz}=\iint\limits_{D}{dxdy}\int\limits_{{{\phi }_{1}}\left( x \right)}^{{{\phi }_{2}}\left( x \right)}{f\left( x;\ y;\ z \right)dz}$

Внутренний интеграл 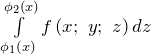$\int\limits_{{{\phi }_{1}}\left( x \right)}^{{{\phi }_{2}}\left( x \right)}{f\left( x;\ y;\ z \right)dz}$ вычисляется по переменной $z$ , а переменные $x$ и $y$ в этом случае считаются постоянными. Результатом интегрирования есть функция переменных $x$ и $y$ – $F\left( x;y \right)$ . Итак, вычисление тройного интеграла сводится к вычислению двойного интеграла $\iint\limits_{D}{F\left( x;\ y \right)dxdy}$ .

ЗАМЕЧАНИЕ

Порядок интегрирования в тройном интеграле может быть изменен, то есть внутренний интеграл может находиться как по переменной $x$ , так и по переменной $y$ .

Примеры решения задач

ПРИМЕР 1

Задание

Вычислить тройной интеграл $I=\iiint\limits_{\Omega }{xdxdydz}$ , где область $\Omega$ – это тетраэдр, ограниченный плоскостью $2x+2y+z-6=0$ и координатными плоскостями.

Решение

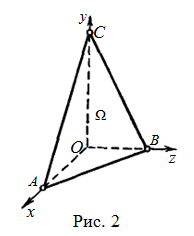
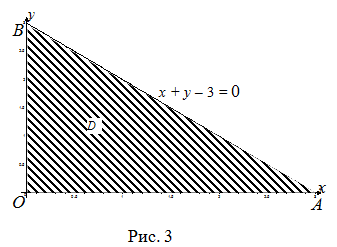
Вычисление интеграла начнем с того, что изобразим заданную область $\Omega$ . Заданий тетраэдр снизу ограничен координатной плоскостью $Oxy$ , уравнение которой $z=0$ , сверху плоскостью $2x+2y+z-6=0$ , а по бокам координатными плоскостями $Oxz\ \left( y=0 \right)$ и $Oyz\ \left( x=0 \right)$ (рис. 2).

Из уравнения $2x+2y+z-6=0$ плоскости находим $z=6-2x-2y$ . Таким образом, можно сделать вывод, что в области $\Omega$ переменная $z$ изменяется от 0 до $6-2x-2y$ : $0\le z\le 6-2x-2y$ .

Для нахождения пределов для переменных $x$ и $y$ спроектируем пространственную область $\Omega$ на плоскость $Oxy$ . Проекцией будет треугольник $AOB$ (рис. 3), ограниченный координатными прямыми и прямой $AB$ . Найдем уравнение этой прямой:

$\left( AB \right):\left\{ \begin{matrix} 2x+2y+z-6=0, \\ z=0 \\ \end{matrix} \right.\Rightarrow 2x+2y-6=0\Rightarrow x+y-3=0\Rightarrow y=3-x$

Таким образом, область $D$ , определяется неравенствами $D:\left\{ \begin{matrix} 0\le x\le 3, \\ 0\le y\le 3-x. \\ \end{matrix} \right.$

Тогда будем иметь:

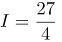$I=\int\limits_{0}^{3}{dx}\int\limits_{0}^{3-x}{dy}\int\limits_{0}^{6-2x-2y}{xdz}=\int\limits_{0}^{3}{xdx}\int\limits_{0}^{3-x}{\left. z_{{}}^{{}} \right|_{0}^{6-2x-2y}dy}=\int\limits_{0}^{3}{xdx}\int\limits_{0}^{3-x}{\left( 6-2x-2y \right)dy}=$

$=\int\limits_{0}^{3}{x\left. \cdot \left( 6y-2xy-{{y}^{2}} \right) \right|_{0}^{3-x}dx}=\int\limits_{0}^{3}{x\left( 6\left( 3-x \right)-2x\left( 3-x \right)-{{\left( 3-x \right)}^{2}} \right)dx=}$

$=\int\limits_{0}^{3}{\left( {{x}^{3}}-6{{x}^{2}}+9x \right)dx=}\left. \left( \frac{{{x}^{4}}}{4}-\frac{6{{x}^{3}}}{3}+\frac{9{{x}^{2}}}{2} \right) \right|_{0}^{3}=\frac{81}{4}-54+\frac{81}{2}=\frac{27}{4}$

Ответ

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Тройной интеграл

Примеры решения задач