Перемножение матриц
При умножении матриц ![]() и
и ![]() получается матрица
получается матрица ![]() которая называется произведением матриц и имеет размерность
которая называется произведением матриц и имеет размерность ![]() Элементы матрицы
Элементы матрицы ![]() находятся по следующему правилу: элемент
находятся по следующему правилу: элемент ![]() равен сумме попарных произведений элементов
равен сумме попарных произведений элементов ![]() -той строки матрицы
-той строки матрицы ![]() и
и ![]() -того столбца матрицы
-того столбца матрицы ![]()
Перемножение двух матриц ![]() на
на ![]() осуществляется только в том случае, если число столбцов в матрице
осуществляется только в том случае, если число столбцов в матрице ![]() совпадает с числом строк в матрице
совпадает с числом строк в матрице ![]()
| Задание | Перемножить матрицы |
| Решение | При умножении матрицы При умножении матрицы |
| Ответ | 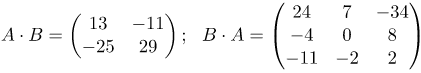 |
Свойства перемножения матриц
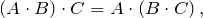
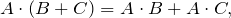
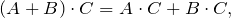
- Для единичной матрицы
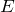 справедливы равенства:
справедливы равенства: 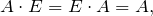
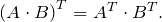
Здесь ![]()
![]()
![]() – произвольные матрицы, для которых указанные равенства имеют смысл.
– произвольные матрицы, для которых указанные равенства имеют смысл.
В общем случае, операция перемножения матриц не является коммутативной, то есть ![]() Матрицы
Матрицы ![]() и
и ![]() для которых это равенство выполняется, называются перестановочными.
для которых это равенство выполняется, называются перестановочными.






![Rendered by QuickLaTeX.com \[A=\left( \begin{matrix} \begin{matrix} -1 & 0 & 2 \\ \end{matrix} \\ \begin{matrix} 3 & 1 & -4 \\ \end{matrix} \\ \end{matrix} \right); \qquad B=\left( \begin{matrix} \begin{matrix} -3 & 7 \\ \end{matrix} \\ \begin{matrix} 4 & 0 \\ \end{matrix} \\ \begin{matrix} 5 & -2 \\ \end{matrix} \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-46d3f06a200c94bb953c0c94e8b1ff60_l3.png)
![Rendered by QuickLaTeX.com \[\begin{matrix} A \cdot B =\left( \begin{matrix} \begin{matrix} -1 & 0 & 2 \\ \end{matrix} \\ \begin{matrix} 3 & 1 & -4 \\ \end{matrix} \\ \end{matrix} \right)\left( \begin{matrix} \begin{matrix} -3 & 7 \\ \end{matrix} \\ \begin{matrix} 4 & 0 \\ \end{matrix} \\ \begin{matrix} 5 & -2 \\ \end{matrix} \\ \end{matrix} \right)=\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-690b720bbc6b733711f5a1362eb86915_l3.png)
![Rendered by QuickLaTeX.com \[\begin{matrix} B \cdot A =\left( \begin{matrix} \begin{matrix} -3 & 7 \\ \end{matrix} \\ \begin{matrix} 4 & 0 \\ \end{matrix} \\ \begin{matrix} 5 & -2 \\ \end{matrix} \\ \end{matrix} \right)\left( \begin{matrix} \begin{matrix} -1 & 0 & 2 \\ \end{matrix} \\ \begin{matrix} 3 & 1 & -4 \\ \end{matrix} \\ \end{matrix} \right)=\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-01b1319c252a961f056f53a15f8a6a0d_l3.png)
![Rendered by QuickLaTeX.com \[=\left( \begin{matrix} -3\cdot \left( -1 \right)+7\cdot 3 & -3\cdot 0+7\cdot 1 & -3\cdot 2+7\cdot \left( -4 \right) \\ 4\cdot \left( -1 \right)+0\cdot 3 & 4\cdot 0+0\cdot 1 & 4\cdot 2+0\cdot \left( -4 \right) \\ 5\cdot \left( -1 \right)+\left( -2 \right)\cdot 3 & 5\cdot 0+\left( -2 \right)\cdot 1 & 5\cdot 2+\left( -2 \right)\cdot \left( -4 \right) \\ \end{matrix} \right)=\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-7393e64d2e02d448bc8020905ca3cefa_l3.png)
![Rendered by QuickLaTeX.com \[ =\left( \begin{matrix} 3+21 & 0+7 & -6-28 \\ -4+0 & 0+0 & 8+0 \\ -5-6 & 0-2 & 10-8 \\ \end{matrix} \right)=\left( \begin{matrix} 24 & 7 & -34 \\ -4 & 0 & 8 \\ -11 & -2 & 2 \\ \end{matrix} \right) \\ \end{matrix}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1aa8774276032ffce6a7513ca2fe9a98_l3.png)





