Примеры решения матриц
Для матриц введены такие основные операции:
- сложение и вычитание матриц;
- умножение матриц на число;
- умножение матрицы на матрицу.
Так же для матриц существуют такие понятия как транспонированная матрица и обратная матрица.
Примеры
| Задание | Даны матрицы |
| Решение | Найдем Вычислим Сначала умножим матрицы на соответствующие числа, для этого каждый элемент первой матрицы умножим на 2, а каждый элемент второй матрицы – на 3. В результате будем иметь: Вычтем полученные матрицы, для этого из соответствующих элементов первой матрицы вычтем соответствующие элементы второй матрицы: |
| Ответ | 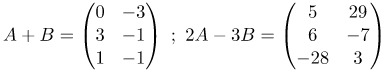 |
| Задание | Заданы матрицы |
| Решение | При нахождении произведения Аналогично найдем произведение |
| Ответ | 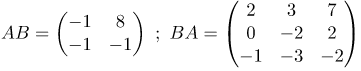 |
| Задание | Найти обратную матрицу для матрицы |
| Решение | Для того, чтобы матрица была обратима, её определитель должен быть ненулевым. Найдем определитель исходной матрицы третьего порядка, используя правило треугольника:
Определитель не равен нулю, следовательно, исходная матрица обратима. Обратную матрицу будем искать по формуле где Найдем все алгебраические дополнения: Подставляя все в формулу для нахождения обратной матрицы, получим |
| Ответ | 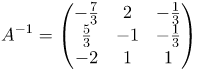 |
| Задание | Найти методом Гаусса обратную матрицу для матрицы |
| Решение | Запишем исходную матрицу и единичную матрицу рядом через черту:
Используя элементарные преобразования строк, приведем левую матрицу к единичной матрице. Из первой строки вычтем вторую строку: Далее, из второй строки вычтем первую, а из третьей строки вычтем первую, умноженную на 3: Из третьей строки вычтем две вторых строки: Умножив вторую и третью строки на К первой строке прибавим третью, ко второй прибавим третью умноженную на 3: Из первой строки вычтем вторую строку: Полученная справа от черты матрица и будет обратной для исходной матрицы. |
| Ответ | 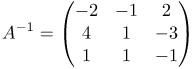 |






![Rendered by QuickLaTeX.com \[ A = \begin{pmatrix} 1 & 4 \\ 3 & -2 \\ -5 & 0 \end{pmatrix} \text{ };\text{ } B = \begin{pmatrix} -1 & -7 \\ 0 & 1 \\ 6 & -1 \end{pmatrix} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-fb84e660ba72dd40059cf1cd46b62420_l3.png)
![Rendered by QuickLaTeX.com \[ A+B = \begin{pmatrix} 1 & 4 \\ 3 & -2 \\ -5 & 0 \end{pmatrix} + \begin{pmatrix} -1 & -7 \\ 0 & 1 \\ 6 & -1 \end{pmatrix} = \begin{pmatrix} 1+(-1) & 4+(-7) \\ 3+0 & -2+1 \\ -5+6 & 0+(-1) \end{pmatrix} = \begin{pmatrix} 0 & -3 \\ 3 & -1 \\ 1 & -1 \end{pmatrix} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-a91057865dccc9406d3dcd03a6929ea4_l3.png)
![Rendered by QuickLaTeX.com \[ 2A-3B = 2 \cdot \begin{pmatrix} 1 & 4 \\ 3 & -2 \\ -5 & 0 \end{pmatrix} - 3 \cdot \begin{pmatrix} -1 & -7 \\ 0 & 1 \\ 6 & -1 \end{pmatrix} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-4208a93b8780b11c8f2d083ef7db2e41_l3.png)
![Rendered by QuickLaTeX.com \[ 2A-3B = \begin{pmatrix} 2 \cdot 1 & 2 \cdot 4 \\ 2 \cdot 3 & 2 \cdot (-2) \\ 2 \cdot (-5) & 2 \cdot 0 \end{pmatrix} - \begin{pmatrix} 3 \cdot (-1) & 3 \cdot (-7) \\ 3 \cdot 0 & 3 \cdot 1 \\ 3 \cdot 6 & 3 \cdot (-1) \end{pmatrix} = \begin{pmatrix} 2 & 8 \\ 6 & -4 \\ -10 & 0 \end{pmatrix} - \begin{pmatrix} -3 & -21 \\ 0 & 3 \\ 18 & -3 \end{pmatrix} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-976ce833172b62111038515c90bbaa5b_l3.png)
![Rendered by QuickLaTeX.com \[ 2A-3B = \begin{pmatrix} 2 & 8 \\ 6 & -4 \\ -10 & 0 \end{pmatrix} - \begin{pmatrix} -3 & -21 \\ 0 & 3 \\ 18 & -3 \end{pmatrix} = \begin{pmatrix} 2-(-3) & 8-(-21) \\ 6-0 & -4-3 \\ -10-18 & 0-(-3) \end{pmatrix} = \begin{pmatrix} 5 & 29 \\ 6 & -7 \\ -28 & 3 \end{pmatrix} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-607970426d0a11373441d2778a7c1535_l3.png)
![Rendered by QuickLaTeX.com \[ A = \begin{pmatrix} 1 & 2 & 3 \\ 0 & -1 & 1 \end{pmatrix} \text{ };\text{ } B = \begin{pmatrix} 2 & 1 \\ 0 & 2 \\ -1 & 1 \end{pmatrix} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-60f9ccab0413ef7bc3e0a817b528979d_l3.png)
![Rendered by QuickLaTeX.com \[ AB = \begin{pmatrix} 1 & 2 & 3 \\ 0 & -1 & 1 \end{pmatrix} \begin{pmatrix} 2 & 1 \\ 0 & 2 \\ -1 & 1 \end{pmatrix} = \begin{pmatrix} 1 \cdot 2 + 2 \cdot 0 + 3 \cdot (-1) & 1 \cdot 1 + 2 \cdot 2 + 3 \cdot 1 \\ 0 \cdot 2 + (-1) \cdot 0 + 1 \cdot (-1) & 0 \cdot 1 + (-1) \cdot 2 + 1 \cdot 1 \end{pmatrix} = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-db3a017540705c2263cdb189e8b3bae4_l3.png)
![Rendered by QuickLaTeX.com \[ BA = \begin{pmatrix} 2 & 1 \\ 0 & 2 \\ -1 & 1 \end{pmatrix} \begin{pmatrix} 1 & 2 & 3 \\ 0 & -1 & 1 \end{pmatrix} = \begin{pmatrix} 2 \cdot 1 + 1 \cdot 0 & 2 \cdot 2 + 1 \cdot (-1) & 2 \cdot 3 + 1 \cdot 1 \\ 0 \cdot 1 + 2 \cdot 0 & 0 \cdot 2 + 2 \cdot (-1) & 0 \cdot 3 + 2 \cdot 1 \\ -1 \cdot 1 + 1 \cdot 0 & -1 \cdot 2 + 1 \cdot (-1) & -1 \cdot 3 + 1 \cdot 1 \end{pmatrix} = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-892d973cf4596dd218912fbeced11cba_l3.png)
![Rendered by QuickLaTeX.com \[ = \begin{pmatrix} 2 & 3 & 7 \\ 0 & -2 & 2 \\ -1 & -3 & -2 \end{pmatrix} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-5113acf88933ac83dbc2f3c3feea7020_l3.png)
![Rendered by QuickLaTeX.com \[ A = \begin{pmatrix} 2 & 7 & 3 \\ 3 & 9 & 4 \\ 1 & 5 & 3 \end{pmatrix} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-7b2159309c19e7e2c2c76948d38caba2_l3.png)
![Rendered by QuickLaTeX.com \[ \det A = \begin{vmatrix} 2 & 7 & 3 \\ 3 & 9 & 4 \\ 1 & 5 & 3 \end{vmatrix} = 2 \cdot 9 \cdot 3 + 1 \cdot 7 \cdot 4 + 3 \cdot 5 \cdot 3 - 1 \cdot 9 \cdot 3 - \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1c97e4fd534e3f7219d83b629e6a47fb_l3.png)
![Rendered by QuickLaTeX.com \[ A^{-1} = \frac{1}{\det A} \begin{pmatrix} A_{11} & A_{21} & A_{31} \\ A_{12} & A_{22} & A_{32} \\ A_{13} & A_{23} & A_{33} \end{pmatrix} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-c03e5296b6c2bb3b2c74f49da9cd36f3_l3.png)
![Rendered by QuickLaTeX.com \[ A^{-1} = \frac{1}{-3} \begin{pmatrix} 7 & -6 & 1 \\ -5 & 3 & 1 \\ 6 & -3 & -3 \end{pmatrix} = \begin{pmatrix} -\frac{7}{3} & 2 &-\frac{1}{3} \\ \frac{5}{3} & -1 & -\frac{1}{3} \\ -2 & 1 & 1 \end{pmatrix} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-298c5da9b925d253cd223e1cf6855355_l3.png)
![Rendered by QuickLaTeX.com \[ A = \begin{pmatrix} 2 & 1 & 1 \\ 1 & 0 & 2 \\ 3 & 1 & 2 \end{pmatrix} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-6e03326ba02decb038bb541a68e0995b_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{pmatrix} 2 & 1 & 1 & 1 & 0 & 0 \\ 1 & 0 & 2 & 0 & 1 & 0 \\ 3 & 1 & 2 & 0 & 0 & 1 \end{pmatrix} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-3c54303d9a2eed3c32fd117207b127e4_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{pmatrix} 2 & 1 & 1 & 1 & 0 & 0 \\ 1 & 0 & 2 & 0 & 1 & 0 \\ 3 & 1 & 2 & 0 & 0 & 1 \end{pmatrix} ~ \begin{pmatrix} 1 & 1 & -1 & 1 & -1 & 0 \\ 1 & 0 & 2 & 0 & 1 & 0 \\ 3 & 1 & 2 & 0 & 0 & 1 \end{pmatrix} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b69aa232fe9e677a9d51ac789105b2c4_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{pmatrix} 1 & 1 & -1 & 1 & -1 & 0 \\ 1 & 0 & 2 & 0 & 1 & 0 \\ 3 & 1 & 2 & 0 & 0 & 1 \end{pmatrix} ~ \begin{pmatrix} 1 & 1 & -1 & 1 & -1 & 0 \\ 0 & -1 & 3 & -1 & 2 & 0 \\ 0 & -2 & 5 & -3 & 3 & 1 \end{pmatrix} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d6dd8c1abee228c48464ce15f7d6db6d_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{pmatrix} 1 & 1 & -1 & 1 & -1 & 0 \\ 0 & -1 & 3 & -1 & 2 & 0 \\ 0 & -2 & 5 & -3 & 3 & 1 \end{pmatrix} ~ \begin{pmatrix} 1 & 1 & -1 & 1 & -1 & 0 \\ 0 & -1 & 3 & -1 & 2 & 0 \\ 0 & 0 & -1 & -1 & -1 & 1 \end{pmatrix} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-4cd94a84a859878cf4bbf4e7ff9bdf56_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{pmatrix} 1 & 1 & -1 & 1 & -1 & 0 \\ 0 & -1 & 3 & -1 & 2 & 0 \\ 0 & 0 & -1 & -1 & -1 & 1 \end{pmatrix} ~ \begin{pmatrix} 1 & 1 & -1 & 1 & -1 & 0 \\ 0 & 1 & -3 & 1 & -2 & 0 \\ 0 & 0 & 1 & 1 & 1 & -1 \end{pmatrix} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-fbcb8e24b6d7625c253dde8b88003562_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{pmatrix} 1 & 1 & -1 & 1 & -1 & 0 \\ 0 & 1 & -3 & 1 & -2 & 0 \\ 0 & 0 & 1 & 1 & 1 & -1 \end{pmatrix} ~ \begin{pmatrix} 1 & 1 & 0 & 2 & 0 & -1 \\ 0 & 1 & 0 & 4 & 1 & -3 \\ 0 & 0 & 1 & 1 & 1 & -1 \end{pmatrix} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-05b8036fd2005cf2a2a3dc7262c90011_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{pmatrix} 1 & 1 & 0 & 2 & 0 & -1 \\ 0 & 1 & 0 & 4 & 1 & -3 \\ 0 & 0 & 1 & 1 & 1 & -1 \end{pmatrix} ~ \begin{pmatrix} 1 & 0 & 0 & -2 & -1 & 2 \\ 0 & 1 & 0 & 4 & 1 & -3 \\ 0 & 0 & 1 & 1 & 1 & -1 \end{pmatrix} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-26d6e50c8aa2d85a470bdeee757932ca_l3.png)





