Примеры решения систем методом Крамера

Метод Крамера – это метод решения систем линейных уравнений. Он применяется только к системам линейных уравнений, у которых число уравнений совпадает с числом неизвестных и определитель отличен от нуля.

Любая крамеровская система уравнений $n \times m$ имеет единственное решение $(x_{1}, x_{2}, ... , x_{n})$ , которое определяется формулами

$x_{i} = \frac{\Delta _{i}}{\Delta}$

где $\Delta _{i}$ – определитель матрицы, полученной из основной матрицы $A$ заменой $i$ -го столбца на столбец свободных членов системы, а $\Delta$ – определитель основной матрицы. Эта формула называется формулой Крамера.

Примеры

ПРИМЕР 1

Задание

Решить систему методом Крамера

$\begin{cases} x-2y=1 \hfill \\ 3x-4y=7 \end{cases}$

Решение

Запишем основную матрицу системы

$A = \begin{pmatrix} 1 & -2 \\ 3 & -4 \end{pmatrix}$

Найдем её определитель

$\Delta = \begin{vmatrix} 1 & -2 \\ 3 & -4 \end{vmatrix} = 1 \cdot (-4) -3 \cdot (-2) = -4+6=2 \neq 0$

Определитель $\Delta \neq 0$ , следовательно, заданная система может быть решена методом Крамера.

Вычислим определитель $\Delta _{x}$ , для этого заменим первый столбец в основной матрице на столбец свободных членов $B = \begin{pmatrix} 1 \\ 7 \end{pmatrix}$ , получим

$\Delta _{x}= \begin{vmatrix} 1 & -2 \\ 7 & -4 \end{vmatrix} = 1 \cdot (-4) -7 \cdot (-2) = -4+14=10$

Аналогично, заменяя второй столбец основной матрицы на $B = \begin{pmatrix} 1 \\ 7 \end{pmatrix}$ , найдем $\Delta _{y}$ :

$\Delta _{x}= \begin{vmatrix} 1 & 1 \\ 3 & 7 \end{vmatrix} = 1 \cdot 7 -3 \cdot 1 = 7-3=4$

Далее по формуле Крамера находим неизвестные переменные:

$x = \frac{\Delta _{x}}{\Delta} = \frac{10}{2} = 5 \text{ };\text{ } y = \frac{\Delta _{y}}{\Delta} = \frac{4}{2} = 2$

Ответ

$x=5 \text{ };\text{ } y=2$

ПРИМЕР 2

Задание

Решить систему методом Крамера

$\begin{cases} 2x_{1}+3x_{2}+1=0 \\ 3x_{1}+4x_{2}+1=0 \end{cases}$

Решение

В уравнениях системы перенесем свободный член вправо:

$\begin{cases} 2x_{1}+3x_{2}=-1\\ 3x_{1}+4x_{2}=-1 \end{cases}$

Тогда основная матрица $A = \begin{pmatrix} 2 & 3 \\ 3 & 4 \end{pmatrix}$ , а столбец свободных членов $B = \begin{pmatrix} -1 \\ -1 \end{pmatrix}$ .

Найдем определитель матрицы системы:

$\Delta = \begin{vmatrix} 2 & 3 \\ 3 & 4 \end{vmatrix} = 2 \cdot 4 -3 \cdot 3 = 8-9=-1$

Определитель $\Delta \neq 0$ , следовательно, система имеет единственное решение и может быть решена методом Крамера. Заменяя первый столбец на столбец свободных членов, найдем, что

$\Delta _{1}= \begin{vmatrix} -1 & 3 \\ -1 & 4 \end{vmatrix} = -1 \cdot 4 - (-1) \cdot 3 = -4+3=-1$

Заменяя второй столбец основной матрицы на столбец $B = \begin{pmatrix} -1 \\ -1 \end{pmatrix}$ , получаем:

$\Delta _{2}= \begin{vmatrix} 2 & -1 \\ 3 & -1 \end{vmatrix} = 2 \cdot (-1) -3 \cdot (-1) = -2+3=1$

Тогда, по формуле Крамера, решением системы будет

$x_{1} = \frac{\Delta _{1}}{\Delta} = \frac{-1}{-1} = 1 \text{ };\text{ } x_{2} = \frac{\Delta _{2}}{\Delta} = \frac{1}{-1} = -1$

Ответ

$x_{1}=1 \text{ };\text{ } x_{2}=-1$

ПРИМЕР 3

Задание

Решить систему методом Крамера

$\begin{cases} x_{1}+x_{2}-2x_{3}=2 \\ 2x_{1}-3x_{2}-x_{3}=1 \\ x_{1}-4x_{2}+x_{3}=3 \end{cases}$

Решение

Запишем основную матрицу заданной системы

$A = \begin{pmatrix} 1 & 1& -2 \\ 2 & -3 & -1 \\ 1 & -4 & 1 \end{pmatrix}$

и найдем её определитель по правилу треугольника:

$\Delta = \begin{vmatrix} 1 & 1& -2 \\ 2 & -3 & -1 \\ 1 & -4 & 1 \end{vmatrix} = 1 \cdot (-3) \cdot 1 + 1 \cdot (-1) \cdot 1 + 2 \cdot (-2) \cdot (-4) - 1 \cdot (-3) \cdot (-2) - 1 \cdot 2 \cdot 1 -$

$- 1 \cdot (-1) \cdot (-4) = -3-1+16-6-2-4=0$

Определитель основной матрицы равен нулю, следовательно, к данной системе нельзя применить метод Крамера.

Ответ

Данная система не может быть решена методом Крамера.

ПРИМЕР 4

Задание

Решить систему линейных уравнений методом Крамера

$\begin{cases} 2x+3y-z=4 \\ x+y+3z=5 \\ 3x-4y+z=0 \end{cases}$

Решение

Найдем определитель основной матрицы системы

$\Delta = \begin{vmatrix} 2 & 3 & -1 \\ 1 & 1 & 3 \\ 3 & -4 & 1 \end{vmatrix} = 2 \cdot 1 \cdot 1 + 3 \cdot 3 \cdot 3 + 1 \cdot (-1) \cdot (-4) - 3 \cdot 1 \cdot (-1) - 1 \cdot 3 \cdot 1 -$

$- 2 \cdot 3 \cdot (-4) = 2 + 27+4+3-3+24=57 \neq 0$

Найдем определитель $\Delta _{x}$ , для этого подставим в последний определитель вместо первого столбца столбец свободных членов $B = \begin{pmatrix} 4 \\ 5 \\ 0 \end{pmatrix}$ :

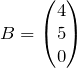$\Delta _{x}= \begin{vmatrix} 4 & 3 & -1 \\ 5 & 1 & 3 \\ 0 & -4 & 1 \end{vmatrix} = 4 \cdot 1 \cdot 1 + 3 \cdot 3 \cdot 0 + 5 \cdot (-1) \cdot (-4) - 0 \cdot 1 \cdot (-1) - 5 \cdot 3 \cdot 1 -$

$- 4 \cdot 3 \cdot (-4) = 4+0+20+0-15+48=57$

Подставляя вместо второго столбца столбец свободных членов, найдем $\Delta _{y}$ :

$\Delta _{y}= \begin{vmatrix} 2 & 4 & -1 \\ 1 & 5 & 3 \\ 3 & 0 & 1 \end{vmatrix} = 2 \cdot 5 \cdot 1 + 4 \cdot 3 \cdot 3 + 1 \cdot (-1) \cdot 0 - 3 \cdot 5 \cdot (-1) - 1 \cdot 4 \cdot 1 -$

$- 2 \cdot 3 \cdot 0 = 10+36+0+15-4-0=57$

Аналогично найдем $\Delta _{z}$ :

$\Delta _{z} = \begin{vmatrix} 2 & 3 & 4 \\ 1 & 1 & 5 \\ 3 & -4 & 0 \end{vmatrix} = 2 \cdot 1 \cdot 0 + 3 \cdot 5 \cdot 3 + 1 \cdot 4 \cdot (-4) - 3 \cdot 1 \cdot 4 - 1 \cdot 3 \cdot 0 -$

$- 2 \cdot 5 \cdot (-4) = 0+45-16-12-0+40=57$

Далее по формуле Камера находим решение заданной системы

$x = \frac{\Delta _{x}}{\Delta} = \frac{57}{57} = 1 \text{ };\text{ } y = \frac{\Delta _{y}}{\Delta} = \frac{57}{57} = 1 \text{ };\text{ } z = \frac{\Delta _{z}}{\Delta} = \frac{57}{57} = 1$

Ответ

$x=1 \text{ };\text{ } y=1 \text{ };\text{ } z=1$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Примеры решения систем методом Крамера

Примеры