Минор матрицы
Минором ![]() произвольного элемента
произвольного элемента ![]() матрицы
матрицы ![]() -го порядка называется определитель
-го порядка называется определитель ![]() -го порядка, полученный из исходной матрицы вычеркиванием
-го порядка, полученный из исходной матрицы вычеркиванием ![]() -ой строки и
-ой строки и ![]() -го столбца.
-го столбца.
Примеры нахождения минора матрицы
| Задание | Найти миноры элементов главной диагонали матрицы |
| Решение | Минор Аналогично, минор |
| Ответ | 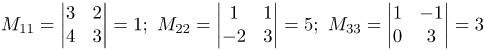 |






![Rendered by QuickLaTeX.com \[ A=\left( \begin{matrix} 1 & -1 & 1 \\ 0 & 3 & 2 \\ -2 & 4 & 3 \\ \end{matrix} \right) \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-2041ebef556b977ac84daf6bf38a9505_l3.png)





