Производная корня икс
![Rendered by QuickLaTeX.com \[ \left( \sqrt{x} \right)' = \frac{1}{2 \sqrt{x}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e75560d21d6c0ca17b165fd077b6806b_l3.png)
Данную формулу можно получить из формулы производной степенной функции ![]() , представив корень в виде дробного показателя:
, представив корень в виде дробного показателя:
![]()
Примеры решения задач по теме «Производная корня»
| Задание | Найти производную функции |
| Решение | Искомая производная
По правилам дифференцирования производная суммы равна сумме производных. То есть тогда Производная первого слагаемого, как константы, равна 0: Найдем производную второго слагаемого Далее находим производную от корня по формуле Производная от суммы равна сумме производных: Первая производная от независимой переменной равна единице, а производная от константы 2 равна нулю, то есть имеем: Итак, |
| Ответ | 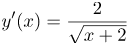 |
| Задание | Найти производную функции |
| Решение | Искомая производная
Производная от корня равна единице деленной на два таких же корня. Но так как подкоренное выражение является сложной функцией (под корнем стоит не просто |
| Ответ | 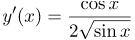 |











