Производная синуса

ОПРЕДЕЛЕНИЕ

Производная синуса равна косинусу того же аргумента.

$\left( \sin x \right)' = \cos x$

То есть синус просто «заменяется» на косинус. Отметим, что производная от косинуса равна минус синусу того же аргумента: $\left( \cos x \right)' = - \sin x$ . Чтобы не запутаться, существует мнемоническое правило для запоминания:

Синий косяк
Косяк – синий

Первая строка показывает нам что производная от синуса равна косинусу (если посмотреть выделенные буквы), а вторая строка дает понять, что производная от косинуса – это минус синус (выделенные буквы и тире).

Примеры решения задач по теме «Производная синуса»

ПРИМЕР 1

Задание

Найти производную функции $y(x) = \sin \sqrt{x}$

Решение

Искомая производная

$y'(x) = \left( \sin \sqrt{x} \right)'$

Аргумент синуса у нас не просто $x$ («икс»), поэтому просто применить приведенную формулу нельзя, так как задана сложная функция. Поэтому производную синуса – косинус такого же аргумента, найденную по выше приведенной формуле, нужно домножить на производную аргумента:

$y'(x) = \left( \sin \sqrt{x} \right)' = \cos \sqrt{x} \cdot \left( \sqrt{x} \right)'$

Производная от корня равна единице деленной на два таких же корня. Тогда имеем:

$y'(x) = \cos \sqrt{x} \cdot \left( \sqrt{x} \right)' = \cos \sqrt{x} \cdot \frac{1}{2 \sqrt{x}} = \frac{\cos \sqrt{x}}{2 \sqrt{x}}$

Ответ

ПРИМЕР 2

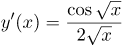Задание

Найти производную функции $y(x) = 2 \sin \left( 3x+4 \right)$

Решение

Искомая производная:

$y'(x) = \left( 2 \sin \left( 3x+4 \right) \right)'$

На первом шаге решения используем правила дифференцирования, а именно то, что константу можно выносить за знак производной:

$y'(x) = \left( 2 \sin \left( 3x+4 \right) \right)' = 2 \left( \sin \left( 3x+4 \right) \right)'$

Далее находим производную от синуса – это косинус такого же аргумента. И так как аргумент есть выражение более сложное, чем просто $x$ , то имеем дело со сложной функцией, а поэтому еще нужно домножить на производную от аргумента, то есть:

$y'(x) = 2 \left( \sin \left( 3x+4 \right) \right)' = 2 \cdot \cos \left( 3x+4 \right) \cdot \left( 3x+4 \right)'$

Производная от суммы равна сумме производных, тогда:

$y'(x) = 2 \cdot \cos \left( 3x+4 \right) \cdot \left( 3x+4 \right)' = 2 \cdot \cos \left( 3x+4 \right) \cdot \left[ \left( 3x \right)' + \left( 4 \right)' \right]$

Производная $\left( 3x \right)'$ , как производная от константы умноженной на $x$ , равна 3; а производная $\left( 4 \right)'$ – производная константы, равна 0.

Таким образом, имеем:

$y'(x) = 2 \cdot \cos \left( 3x+4 \right) \cdot \left[ \left( 3x \right)' + \left( 4 \right)' \right] = 2 \cos \left( 3x+4 \right) \left[ 3+0 \right] = 6 \cos \left( 3x+4 \right)$

Ответ

$y'(x) = 6 \cos \left( 3x+4 \right)$

Понравился сайт? Расскажи друзьям!