Умножение матрицы на вектор
Умножение матрицы на вектор производится по правилу «строка на столбец». При умножении матрицы на вектор-столбец число столбцов в матрице должно совпадать с числом строк в векторе-столбце. Результатом умножения матрицы на вектор-столбец есть вектор-столбец:
![Rendered by QuickLaTeX.com \[A \cdot B =\left( \begin{matrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \ldots & \ldots & \ldots & \ldots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \\ \end{matrix} \right)\cdot \left( \begin{matrix} b_{1} \\ b_{2} \\ \ldots \\ b_{1n} \\ \end{matrix} \right)=\left( \begin{matrix} a_{11}\cdot b_{1}+a_{12}\cdot b_{2}+\ldots +a_{1n}\cdot b_{n} \\ a_{21}\cdot b_{1}+a_{22}\cdot b_{2}+\ldots +a_{2n}\cdot b_{n} \\ \ldots \quad \ldots \quad \ldots \quad \ldots \quad \ldots \quad \ldots \\ a_{m1}\cdot b_{1}+a_{m2}\cdot b_{2}+\ldots +a_{mn}\cdot b_{n} \\ \end{matrix} \right)=\left( \begin{matrix} c_{1} \\ c_{2} \\ \ldots \\ c_{1m} \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-eb7e8c525c1007d9bf4111bc3699f761_l3.png)
При умножении матрицы на вектор-строку, умножаемая матрица может быть только вектором-столбцом, причем количество строк в векторе-столбце должно совпадать с количеством столбцов в векторе-строке. Результатом такого умножения будет квадратная матрица соответствующей размерности:
![Rendered by QuickLaTeX.com \[ A \cdot B =\left( \begin{matrix} a_{1} \\ a_{2} \\ \ldots \\ a_{n} \\ \end{matrix} \right)\cdot \left( b_{1}\quad b_{2}\quad \ldots \quad b_{n} \right)=\left( \begin{matrix} a_{1}\cdot b_{1}\quad a_{1}\cdot b_{2}\quad \ldots \quad a_{1}\cdot b_{n} \\ a_{2}\cdot b_{1}\quad a_{2}\cdot b_{2}\quad \ldots \quad a_{2}\cdot b_{n} \\ \ldots \quad \ldots \quad \ldots \quad \ldots \quad \ldots \quad \ldots \\ a_{n}\cdot b_{1}\quad a_{n}\cdot b_{2}\quad \ldots \quad a_{n}\cdot b_{n} \\ \end{matrix} \right)=\left( \begin{matrix} c_{11} & c_{12} & \ldots & c_{1n} \\ c_{21} & c_{22} & \ldots & c_{2n} \\ \ldots & \ldots & \ldots & \ldots \\ c_{n1} & c_{n2} & \ldots & c_{nn} \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-38a5c3fb9a351f72d11fc82f4ca0c9dd_l3.png)
Примеры умножения матриц на вектора
| Задание | Найти произведение матрицы |
| Решение | По правилу умножения матриц, получим
|
| Ответ | 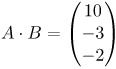 |
| Задание | Найти произведение вектора-столбца |
| Решение | Вектор-столбец и вектор-строка являются разновидностью матриц. Тогда по правилу умножения матриц, получим:
|
| Ответ | 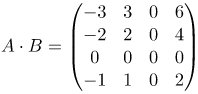 |






![Rendered by QuickLaTeX.com \[A=\left( \begin{matrix} 2 & 4 & 0 \\ -2 & 1 & 3 \\ -1 & 0 & 1 \\ \end{matrix} \right),\text{ } B=\left( \begin{matrix} 1 \\ 2 \\ -1 \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-c0d24519793cd21d9835557816a8e8da_l3.png)
![Rendered by QuickLaTeX.com \[A\cdot B=\left( \begin{matrix} 2 & 4 & 0 \\ -2 & 1 & 3 \\ -1 & 0 & 1 \\ \end{matrix} \right)\cdot \left( \begin{matrix} 1 \\ 2 \\ -1 \\ \end{matrix} \right)=\left( \begin{matrix} 2\cdot 1+4\cdot 2+0\cdot \left( -1 \right) \\ -2\cdot 1+1\cdot 2+3\cdot \left( -1 \right) \\ -1\cdot 1+0\cdot 2+1\cdot \left( -1 \right) \\ \end{matrix} \right)=\left( \begin{matrix} 2+8+0 \\ -2+2-3 \\ -1+0-1 \\ \end{matrix} \right)=\left( \begin{matrix} 10 \\ -3 \\ -2 \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-8d6c06170b0017f7d5403b3dfed9b2d2_l3.png)
![Rendered by QuickLaTeX.com \[ A=\left( \begin{matrix} 3 \\ 2 \\ 0 \\ -1 \\ \end{matrix} \right) ,\text{ } B=\left( \begin{matrix} -1 & 1 & 0 & 2 \\ \end{matrix} \right) \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-db916d56bc81e01c18fe7ea6db943960_l3.png)
![Rendered by QuickLaTeX.com \[A \cdot B =\left( \begin{matrix} 3 \\ 2 \\ 0 \\ 1 \\ \end{matrix} \right)\cdot \left( \begin{matrix} -1 & 1 & 0 & 2 \\ \end{matrix} \right)=\left( \begin{matrix} 3\cdot \left( -1 \right) & 3\cdot 1 & 3\cdot 0 & 3\cdot 2 \\ 2\cdot \left( -1 \right) & 2\cdot 1 & 2\cdot 0 & 2\cdot 2 \\ 0\cdot \left( -1 \right) & 0\cdot 1 & 0\cdot 0 & 0\cdot 2 \\ 1\cdot \left( -1 \right) & 1\cdot 1 & 1\cdot 0 & 1\cdot 2 \\ \end{matrix} \right)=\left( \begin{matrix} -3 & 3 & 0 & 6 \\ -2 & 2 & 0 & 4 \\ 0 & 0 & 0 & 0 \\ -1 & 1 & 0 & 2 \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-4a01beb0fcf773aed5b612b732c8bf56_l3.png)





