Собственные векторы и собственные значения (числа) матрицы
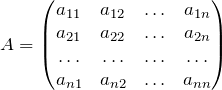 .
Ненулевой вектор
.
Ненулевой вектор 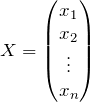 называется собственным вектором матрицы
называется собственным вектором матрицы Число ![]() при этом называется собственным значением вектора
при этом называется собственным значением вектора ![]() относительно матрицы
относительно матрицы ![]() .
.
Матрица ![]() называется характеристической матрицей матрицы
называется характеристической матрицей матрицы ![]() , многочлен
, многочлен ![]() называется характеристическим многочленом матрицы
называется характеристическим многочленом матрицы ![]() , уравнение
, уравнение ![]() называется характеристическим уравнением матрицы
называется характеристическим уравнением матрицы ![]() .
.
Координаты собственного вектора ![]() соответствующего собственному значению
соответствующего собственному значению ![]() находятся из однородной системы уравнений
находятся из однородной системы уравнений
![Rendered by QuickLaTeX.com \[\left\{ \begin{matrix} \left( a_{11}-\lambda \right)x_{1}+a_{12}x_{2}+\ldots +a_{1n}x_{n}=0 \\ a_{21}x_{1}+\left( a_{22}-\lambda \right)x_{2}+\ldots +a_{2}x_{n}=0 \\ \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \\ a_{n1}x_{1}+a_{n2}x_{2}+\ldots +\left( a_{nn}-\lambda \right)x_{n}=0 \\ \end{matrix} \right.\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-524112577c119f70b31778f59b620b1b_l3.png)
Примеры нахождения собственных векторов и значений матрицы
| Задание | Найти собственные векторы и собственные значения матрицы
|
| Решение | Составим характеристическое уравнение Раскроем полученный определитель по правилу треугольника: После раскрытия скобок и приведения подобных получим характеристический многочлен Раскладываем полученный многочлен на множители: Тогда или Таким образом, исходная матрица имеет одно действительное собственное значение Для отыскания собственного вектора подставим найденное собственное значение получим Решим полученную однородную систему уравнений методом Гаусса. Выпишем основную матрицу этой системы Преобразуем её с помощью элементарных преобразований. Умножим третью строку на Поменяем местами первую и третью строки: Прибавим ко второй строке первую и к третьей строке прибавим первую строку, умноженную на К третьей строке прибавим первую строку, умноженную на Умножим вторую строку на Переходя обратно к системе, будем иметь: Полагая |
| Ответ |  |






![Rendered by QuickLaTeX.com \[A=\left( \begin{matrix} 4 & -5 & 7 \\ 1 & -4 & 9 \\ -4 & 0 & 5 \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-534e1be728702a8210c4ed28773f8700_l3.png)
![Rendered by QuickLaTeX.com \[\left| \begin{matrix} 4-\lambda & -5 & 7 \\ 1 & -4-\lambda & 9 \\ -4 & 0 & 5-\lambda \\ \end{matrix} \right|=0\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-8dc52daf2db2c9e2a9cfd7a74b534e80_l3.png)
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{rcl} \left( 4-\lambda \right)x_{1}+5x_{2}+7x_{3}=0 \\ x_{1}+\left( 4.+\lambda \right)x_{2}+9x_{3}=0 \\ -4x_{1}+\left( 5-\lambda \right)x_{3}=0 \\ \end{array} \right.\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b4306fc43f4c8696c90ab1ae53460dde_l3.png)
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{rcl} 3x_{1}-5x_{2}+7x_{3}=0 \\ x_{1}-5x_{2}+9x_{3}=0 \\ -4x_{1}+4x_{3}=0 \\ \end{array} \right.\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-3f6283aac0d84bca5258022eaadad0ac_l3.png)
![Rendered by QuickLaTeX.com \[\left( \begin{matrix} 3 & -5 & 7 \\ 1 & -5 & 9 \\ -4 & 0 & 4 \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-6d7ef967fd8d9d26b1d49c47857ceefb_l3.png)
![Rendered by QuickLaTeX.com \[\left( \begin{matrix} 3 & -5 & 7 \\ 1 & -5 & 9 \\ -4 & 0 & 4 \\ \end{matrix} \right)\sim\left( \begin{matrix} 3 & -5 & 7 \\ 1 & -5 & 9 \\ -1 & 0 & 1 \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e6b090ba584281b0f43b4835d3b2ada4_l3.png)
![Rendered by QuickLaTeX.com \[\left( \begin{matrix} 3 & -5 & 7 \\ 1 & -5 & 9 \\ -1 & 0 & 1 \\ \end{matrix} \right)\sim\left( \begin{matrix} -1 & 0 & 1 \\ 1 & -5 & 9 \\ 3 & -5 & 7 \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e3eff0648b361a100dfe2c40ca814c1b_l3.png)
![Rendered by QuickLaTeX.com \[\left( \begin{matrix} -1 & 0 & 1 \\ 1 & -5 & 9 \\ 3 & -5 & 7 \\ \end{matrix} \right)\sim\left( \begin{matrix} -1 & 0 & 1 \\ 0 & -5 & 10 \\ 0 & -5 & 10 \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d7587539cf16f1e807be7fd4785536f9_l3.png)
![Rendered by QuickLaTeX.com \[\left( \begin{matrix} -1 & 0 & 1 \\ 0 & -5 & 10 \\ 0 & -5 & 10 \\ \end{matrix} \right)\sim\left( \begin{matrix} -1 & 0 & 1 \\ 0 & -5 & 10 \\ 0 & 0 & 0 \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-bdbb001c126d91c73658822336660f19_l3.png)
![Rendered by QuickLaTeX.com \[\left( \begin{matrix} -1 & 0 & 1 \\ 0 & -5 & 10 \\ 0 & 0 & 0 \\ \end{matrix} \right)\sim\left( \begin{matrix} -1 & 0 & 1 \\ 0 & 1 & -2 \\ 0 & 0 & 0 \\ \end{matrix} \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-912d9aef5892b8de37705092c905df20_l3.png)





