Примеры решения логарифмических неравенств
Теория по логарифмическим неравенствам
Решение логарифмических неравенств основывается на свойстве монотонности логарифмической функции: функция ![]() монотонно возрастает, если
монотонно возрастает, если ![]() , и монотонно убывает, если
, и монотонно убывает, если ![]() . При этом учитывается, что подлогарифмическое выражение может принимать только положительные значения. Таким образом, для неравенства вида
. При этом учитывается, что подлогарифмическое выражение может принимать только положительные значения. Таким образом, для неравенства вида
![]()
при потенцировании, для значений ![]() знак неравенства сохраняется; а для значений
знак неравенства сохраняется; а для значений ![]() , меняется на противоположный.
, меняется на противоположный.
В случае если переменная содержится и в основании, и в подлогарифмическом выражении, например ![]() , решение разбивается два случая, когда
, решение разбивается два случая, когда ![]() и, когда
и, когда ![]() , то есть
, то есть
![Rendered by QuickLaTeX.com \[ \log _{\varphi (x)} f(x) > \log _{\varphi (x)} g(x) = \left[ \begin{gathered} \begin{cases} \varphi (x)>1 \\ 0<g(x)<f(x) \end{cases} \\ \begin{cases} 0< \varphi (x) <1 \\ 0<f(x)<g(x) \end{cases} \end{gathered} \right \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9c88a13154a2e436d0acba27fad5809a_l3.png)
Так же некоторые логарифмические неравенства можно решить методом замены переменной.
Примеры
| Задание | Решить неравенство |
| Решение | ОДЗ:
Умножим правую часть на По свойствам логарифмов, внесем коэффициент –2 как степень подлогарифмического выражения: Далее переходим к подлогарифмическим выражением и, так как основание логарифма Полученный интервал полностью принадлежит области допустимых значений, поэтому он и является решением заданного неравенства. |
| Ответ |
| Задание | Решить неравенство |
| Решение | ОДЗ:
Умножая правую часть на По свойствам логарифмов, коэффициент 4 можно внести под знак логарифма как степень подлогарифмического выражения: Далее потенцируем по основанию 2 и, так как основание логарифма Данный интервал попадает в область допустимых значений, поэтому является решением. |
| Ответ |
| Задание | Решить неравенство |
| Решение | Определим область допустимых значений:
Представим правую часть неравенства как После потенцирования по основанию Заменим в последнем неравенстве и пропотенцируем его по основанию 3, так Вычтем из всех частей неравенства 1, получим Полученный промежуток |
| Ответ |
| Задание | Решить неравенство |
| Решение | ОДЗ: Это логарифмическое неравенство решается методом замены переменной. Введем замену , тогда неравенство примет вид: Для решения этого неравенства, сначала найдем корни уравнения Сделаем обратную замену: если 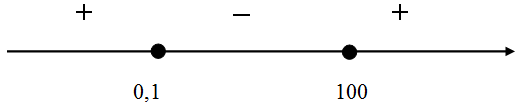
И, так как нас интересуют только те значения |
| Ответ |
| Задание | Найти решение неравенства |
| Решение | Данное неравенство содержит переменную и под знаком логарифма и в основании. Представим правую часть неравенства как Последнее неравенство равносильно совокупности двух систем Решение получим, объединяя эти два промежутка: |
| Ответ | 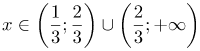 |






![Rendered by QuickLaTeX.com \[ \begin{cases} \log _{3} (x+1) > 0 \\ x+1 > 0 \end{cases} \Rightarrow \begin{cases} \log _{3} (x+1) > \log _{3} 1 \\ x> -1 \end{cases} \Rightarrow \begin{cases} x+1>1 \\ x> -1 \end{cases} \Rightarrow \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-cfe2d4abd705b4c9bf110cfeb7758c82_l3.png)
![Rendered by QuickLaTeX.com \[ \Rightarrow \begin{cases} x>0 \\ x> -1 \end{cases} \text{ } \Rightarrow \text{ } x>0 \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-79d2311c75f80a256356b5a4ae2d720c_l3.png)
![Rendered by QuickLaTeX.com \[ \left[ \begin{gathered} \begin{cases} 0<x<1 \\ 3x-1<1 \\ 3x-1>0 \end{cases} \\ \begin{cases} x>1 \\ 3x-1>1 \end{cases} \end{gathered} \right \text{ } \Rightarrow \text{ } \left[ \begin{gathered} \begin{cases} 0<x<1 \\ 3x<2 \\ 3x>1 \end{cases} \\ \begin{cases} x>1 \\ 3x>2 \end{cases} \hfill \end{gathered} \right \text{ } \Rightarrow \text{ } \left[ \begin{gathered} \begin{cases} 0<x<1 \\ x<\frac{2}{3} \\ x>\frac{1}{3} \end{cases} \\ \begin{cases} x>1 \\ x>\frac{2}{3} \end{cases} \hfill \end{gathered} \right \text{ } \Rightarrow \text{ } \left[ \begin{gathered} \frac{1}{3}<x<\frac{2}{3} \\ x>\frac{2}{3} \end{cases} \end{gathered} \right \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-5e2fcf50990067568816fe50c2a177b4_l3.png)





