Метод рационализации при решении неравенств
При решении сложных неравенств часто применяют метод рационализации, т.е. приведение неравенства к более простому виду, а именно, к рациональному неравенству. Это позволяет использовать для его решения метод интервалов. Этот метод применяют к решению логарифмических, показательных и иррациональных неравенств.
Метод рационализации заключается в том, что если некоторая функция ![]() монотонно возрастает, а точки
монотонно возрастает, а точки ![]() и
и ![]() принадлежат области определения функции, то разность
принадлежат области определения функции, то разность ![]() совпадает по знаку с разностью
совпадает по знаку с разностью ![]() .
.
Например, неравенство ![]() можно заменить на равносильное ему
можно заменить на равносильное ему ![]() . Решая упрощенное неравенство необходимо учитывать ОДЗ функций, входящих в исходное неравенство.
. Решая упрощенное неравенство необходимо учитывать ОДЗ функций, входящих в исходное неравенство.
Примеры решения неравенств методом рационализации
| Задание | Решить неравенство
|
| Решение | Показательные функции Получили дробно-рациональное неравенство, которое решим методом интервалов 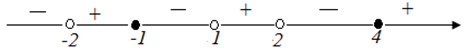
Выбирает интервалы со знаком «минус»: |
| Ответ |
| Задание | Решить логарифмическое неравенство методом рационализации |
| Решение | В заданном неравенстве перейдем к новому основанию логарифма, например к десятичному логарифму
Перенесем единицу в левую часть и приведем к общему знаменателю Поскольку Логарифм является монотонно возрастающей функцией, поэтому можно применить метод рационализации и заменить полученное неравенство равносильным С учетом ОДЗ исходного неравенства получим систему неравенств Первое неравенство решим методом интервалов 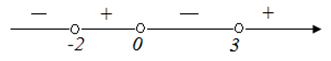
Итак, решением данного неравенства будет интервал |
| Ответ |






![Rendered by QuickLaTeX.com \[\left\{\begin{array}{l} {\frac{x^{2} -x-6}{x} >0,} \\ {x^{2} -5>0,} \\ {\begin{array}{l} {x+1>0,} \\ {x+1\ne 1} \end{array}} \end{array}\ \Rightarrow \ \right. \left\{\begin{array}{l} {\frac{(x-3)(x+2)}{x} >0,} \\ {(x-\sqrt{5} )(x+\sqrt{5} )>0,} \\ {\begin{array}{l} {x>-1,} \\ {x\ne 0} \end{array}} \end{array}\ \Rightarrow \ \left\{\begin{array}{l} {\frac{(x-3)(x+2)}{x} >0,} \\ {x\in (\sqrt{5} ;+\infty )} \end{array}\right. \right. \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-82d30997bff46e86872b152b66f930b6_l3.png)





