Производная арккотангенса
![Rendered by QuickLaTeX.com \[ \left( \text{arcctg} x \right)' = -\frac{1}{1+x^{2}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-81aab625cda4d21c44d4acde61332eff_l3.png)
Как можно заметить, производная арккотангенса отличается от производной арктангенса только знаком.
Функция ![]() является обратной к функции
является обратной к функции ![]() . Если аргумент арккотангенса отличен от просто «икс», то его производная находится по формуле:
. Если аргумент арккотангенса отличен от просто «икс», то его производная находится по формуле:
![]()
Примеры решения задач
| Задание | Найти производную функции |
| Решение | Искомая производная
По свойству производных производная суммы равна сумме производных от каждого из слагаемых, то есть Производная от первого слагаемого Производная второго слагаемого Таким образом, |
| Ответ | 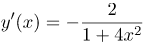 |
| Задание | Найти производную функции |
| Решение | Производная заданной функции:
Производная натурального логарифма равна единице деленной на подлогарифмическую функцию: Производная от логарифма была умножена еще на производную от его аргумента, так как подлогарифмическая функция отлична от Находим теперь производную от арккотангенса: |
| Ответ | 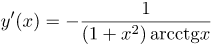 |











