Производная арктангенса
![Rendered by QuickLaTeX.com \[ \left( \text{arctg} x \right)' = \frac{1}{1+x^{2}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-4ad43ce3bd2956828cdb36c54501427a_l3.png)
Данная функция является обратной к функции ![]() . Если аргумент арктангенса есть некоторой функцией
. Если аргумент арктангенса есть некоторой функцией ![]() , то его производная равна
, то его производная равна
![]()
Примеры решения задач по теме «Производная арктангенса»
| Задание | Найти производную функции |
| Решение | Так как аргумент арктангенса есть функцией от где Производная от корня равна единице деленной на два таких же корня: Тогда |
| Ответ | 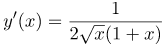 |
| Задание | Найти производную функции |
| Решение | Искомая производная
Заданная функция представляет собой степенную функцию, поэтому производную от нее находим по формуле: Производная суммы равна сумме производных, то есть Производная от первого слагаемого – единицы – равна нулю, как от константы: а производная второго слагаемого Итак, производная заданной функции |
| Ответ | 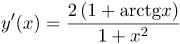 |











