Таблицы истинности

Они могут принимать значения «истина» или «ложь» (1 или 0). Для функции, содержащей две переменные, наборов значений переменных всего четыре:

Значения логических функций определяются с помощью таблица истинности.

Таблицы истинности для основных двоичных логических функций

1. Конъюнкция (логическое умножение) – сложное логическое выражение, которое является истинным только в том случае, когда истинны оба входящих в него простых выражения.

Обозначение:

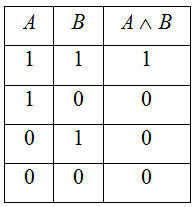
2. Дизъюнкция (логическое сложение) – это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно, если оба простых логических выражения ложны.

Обозначение:

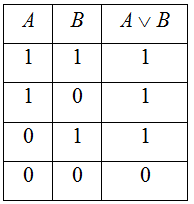
3. Импликация (логическое следствие) – это сложное логическое выражение, которое является ложным тогда и только тогда, когда условие истинно, а следствие ложно.

Обозначение:

4. Эквиваленция – это сложное логическое высказывание, которое является истинным только при одинаковых значениях истинности простых выражений, входящих в него.

Обозначение:

5. Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное – истинным.

Обозначение:

6. Штрих Шеффера – операция, отрицающая конъюнкцию, т.е. значение ложно тогда и только тогда, когда оба простых выражения истинны.

Обозначение:

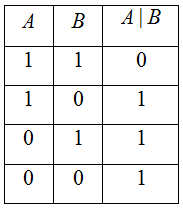
7. Стрелка Пирса – операция, отрицающая конъюнкцию, т.е. значение истинно тогда и только тогда, когда оба простых выражения ложны.

Обозначение:

Порядок выполнения логических операций

При построении таблицы истинности необходимо учитывать порядок выполнения логических операций:

1. Инверсия
2. Конъюнкция
3. Дизъюнкция
4. Импликация
5. Эквиваленция
6. Штрих Шеффера
7. Стрелка Пирса

Для последних двух операций приоритет не определен.

Замечание. Если необходимо изменить указанный порядок выполнения логических операций используются скобки.

Примеры решения задач

ПРИМЕР 1

Задание	Составить таблицу истинности для функции
Решение	Составим таблицу истинности для заданной функции, которая содержит две переменные и . В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных функций и в последнем столбце — значение функций. В результате получим таблицу:

ПРИМЕР 2

Задание	Составить таблицу истинности для функции
Решение	Составим таблицу истинности для заданной функции, которая содержит три переменные и . Наборов возможных переменных будет 8 и запишем их в первых трех столбцах таблицы, в последующих столбцах — значения промежуточных функций и в последнем столбце — значение функций. Промежуточные функции: I – II – III – IV – V – VI – В результате получим таблицу: