Частные производные второго порядка
Если задана функция ![]() и вычислены ее частные производные
и вычислены ее частные производные ![]() и
и ![]() то они в свою очередь также являются функциями независимых переменных
то они в свою очередь также являются функциями независимых переменных ![]() и
и ![]() а поэтому от каждой из них можно найти производную по каждой из переменных.
а поэтому от каждой из них можно найти производную по каждой из переменных.
![]()
Итак,
![]()
Если взять частную производную по переменной ![]() от производной
от производной ![]() то получим частную производную второго порядка функции
то получим частную производную второго порядка функции ![]() , которую взято вначале по переменной
, которую взято вначале по переменной ![]() а потом – по переменной
а потом – по переменной ![]() Такая производная называется смешанной производной и обозначается
Такая производная называется смешанной производной и обозначается
![]()
Аналогично, частная производная по переменной ![]() от первой производной
от первой производной ![]() по переменной
по переменной ![]() дает вторую смешанную частную производную функции
дает вторую смешанную частную производную функции ![]() вычисленную вначале по переменной
вычисленную вначале по переменной ![]() а потом – по переменной
а потом – по переменной ![]() Она обозначается символом
Она обозначается символом
![]()
![]()
Частная производная по переменной ![]() от производной первого порядка
от производной первого порядка ![]() есть второй частной производной от функции
есть второй частной производной от функции ![]() по переменной
по переменной ![]() Ее обозначают следующим образом:
Ее обозначают следующим образом:
![]()
Подобным образом задаются производные более высокого порядка, чем второй. Например, выражение ![]() определяет производную третьего порядка функции
определяет производную третьего порядка функции ![]() найденную три раза по переменной
найденную три раза по переменной ![]() Аналогично
Аналогично ![]() – смешанная производная третьего порядка, взятая два раза по переменной
– смешанная производная третьего порядка, взятая два раза по переменной ![]() и от полученной производной
и от полученной производной ![]() найдена один раз производная по переменной
найдена один раз производная по переменной ![]()
| Задание | Найти все частные производные второго порядка функции |
| Решение | Чтобы найти производные второго порядка, вначале вычислим частные производные первого порядка:
Переходим к нахождению частных производных второго порядка. Для нахождения второй производной Аналогично Смешанные производные: Получили, что Таким же образом находим оставшиеся смешанные производные: Проверка: и равенство |
| Ответ | 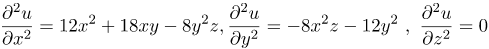 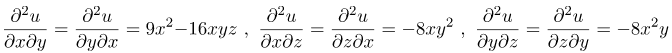 |











