Смешанная производная
![Rendered by QuickLaTeX.com \[ \lim_{\Delta y \to 0}{\frac{\frac{\partial f(x_0; y_0 + \Delta y)}{\partial x} - \frac{\partial f(x_0; y_0)}{\partial x}}{\Delta y}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-eb2be93430b8a86bc83c4b2762799147_l3.png)
если он существует, называется смешанной производной функции ![]() в точке
в точке ![]() и обозначается
и обозначается
![]()
Аналогично определяется ![]() как
как
![Rendered by QuickLaTeX.com \[ \lim_{\Delta x \to 0}{\frac{\frac{\partial f(x_0 + \Delta x; y_0)}{\partial y} - \frac{\partial f(x_0; y_0)}{\partial y}}{\Delta x}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-271ac48965b3d708024906d9268d9a21_l3.png)
если он существует.
Имеют место обозначения:
![]()
![]()
Имеет место теорема о равенстве смешанных производных.
- Функции
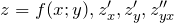 и
и 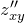 определены в некоторой окрестности точки
определены в некоторой окрестности точки 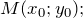
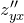 и
и 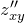 непрерывны в указанной точке.
непрерывны в указанной точке.
Тогда ![]() то есть смешанные производные второго порядка равны в каждой точке, где они непрерывны.
то есть смешанные производные второго порядка равны в каждой точке, где они непрерывны.
Примеры вычисления смешанных производных
| Задание | Найти смешанную производную |
| Решение | Продифференцируем вначале заданную функцию по переменной Для нахождения требуемой производной |
| Ответ |
| Задание | Показать, что для функции |
| Решение | Найдем вначале смешанную производную Аналогично, смешанная производная То есть |
| Ответ |











