Частные производные первого порядка

Пусть функция $z = f(x,y)$ определена в некоторой окрестности точки $M(x, y) .$ Придадим переменной $x$ приращение $\Delta x ,$ оставляя при этом значение переменной $y$ без изменения так, чтобы точка $M_1(x + \Delta x, y)$ принадлежала этой окрестности.

ОПРЕДЕЛЕНИЕ

Величину $\Delta_x z = f(x + \Delta x, y) - f(x, y)$ называют частным приращением функции $f(x, y)$ по переменной $x .$ Аналогично вводится частное приращение $\Delta_y z$ этой функции по переменной $y :$

$\Delta_y z = f(x, y + \Delta y) - f(x, y)$

Если существует предел

$\lim_{\Delta x \to 0} \frac{\Delta_x z}{\Delta x} = \lim_{\Delta x \to 0} \frac{f(x + \Delta x, y) - f(x, y)}{\Delta x}$

то он называется частной производной функции $f(x, y)$ в точке $M(x, y)$ по переменной $x$ и обозначается одним из следующих символов:

$z_x' \text{ },\text{ } f_x' \text{ },\text{ } \frac{\partial z}{\partial x} \text{ },\text{ } \frac{\partial f}{\partial x}$

Аналогично частная производная функции $f(x, y)$ по переменной $y$ определяется как предел

$\lim_{\Delta y \to 0} \frac{\Delta_y z}{\Delta y} = \lim_{\Delta x \to 0} \frac{f(x, y + \Delta y) - f(x, y)}{\Delta y}$

Она обозначается как $z_y', f_y', \frac{\partial z}{\partial y}, \frac{\partial f}{\partial y} .$

Согласно с определением, при нахождении частной производной $z'_x$ находят обыкновенную производную функции одной переменной $x ,$ считая переменную $y$ постоянной, а при нахождении производной $z'_y$ постоянной считается переменная $x .$

Следовательно, частные производные находятся по формулам и правилам дифференцирования функции одной переменной.

Частная производная $z'_x$ характеризует скорость изменения функции в направлении оси $Ox, z'_y$ – в направлении оси $Oy .$

Выясним геометрический смысл частных производных функции двух переменных. Геометрическим образом (графиком) функции $z = f(x, y)$ есть некоторая поверхность. Графиком функции $z = f(x, y_0)$ является линия пересечения этой поверхности с плоскостью $y = y_0 .$ Исходя из геометрического смысла производной функции одной переменной, получаем, что,

$f'_x (x_0, y_0) = \text{tg} \alpha$

где $\alpha$ – угол между осью $Ox$ и касательной, проведенной к пространственной кривой $z = f(x, y_0)$ в точке $M_0 (x_0, y_0, f(x_0, y_0)) .$ Аналогично, $f'_y(x_0, y_0) = \text{tg} \beta ,$ где $\beta$ – угол между осью $Oy$ и касательной, проведенной к пространственной кривой $z = f(x_0, y)$ (линии пересечения поверхности $z = f(x, y)$ с плоскостью $x = x_0$ ) в точке $M_0 (x_0, y_0, f(x_0, y_0)) .$

Для функции $n$ переменных $u = f(x_1, x_2, \ldots, x_n)$ можно найти $n$ частных производных первого порядка:

$\frac{\partial u}{\partial x_1}, \frac{\partial u}{\partial x_2}, \ldots, \frac{\partial u}{\partial x_n}$

Чтобы найти частную производную $\frac{\partial u}{\partial x_i}, i = 1; 2; \ldots; n ,$ необходимо взять обычную производную функции $u = f(x_1, x_2, \ldots, x_n)$ по переменной $x_i ,$ считая остальные переменные константами.

Примеры вычисления частных производных первого порядка

ПРИМЕР 1

Задание

Найти частные производные первого порядка по переменным $x$ и $y$ функции $z = 3x^2y - \frac{x}{y^3} + 2x - 3y + 1 .$

Решение

Найдем частную производную $z'_x .$ Для этого дифференцируем заданную функцию по переменной $x ,$ считая $y$ постоянной величиною:

$z_x' = \left( 3x^2y - \frac{x}{y^3} + 2x - 3y + 1 \right)'_x = (3x^2y)'_x - \left( \frac{x}{y^3} \right)'_x + 2(x)'_x - 3(y)'_x + (1)'_x =$

$= 3y(x^2)'_x - \frac{1}{y^3}(x)'_x + 2 \cdot 1 - 3 \cdot 0 + 0 = 6xy - \frac{1}{y^3} \cdot 1 + 2$

То есть

$z_x' = 6xy - \frac{1}{y^3} + 2$

Находим теперь производную $z_y' ,$ для этого дифференцируем заданную функцию $z = 3x^2y - \frac{x}{y^3} + 2x - 3y + 1$ по $y ,$ при этом переменная $x$ считается константой:

$z_y' = 3x^2 + \frac{3x}{y^4} - 3$

Ответ

ПРИМЕР 2

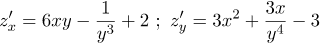Задание

Найти частные производные первого порядка функции

$z = \arcsin \frac{y}{x}$

Решение

Найдем первую частную производную по переменной $x .$ При дифференцировании вторая переменная $y$ будет считаться константой:

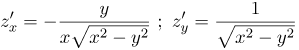$z_x' = \left( \arcsin \frac{y}{x} \right)'_x = \frac{1}{\sqrt{1 - \left( \frac{y}{x} \right)^2}} \cdot \left( \frac{y}{x} \right)'_x = \frac{x}{\sqrt{x^2 - y^2}} \cdot y \cdot \left(\frac{1}{x} \right)'_x =$

$= \frac{xy}{\sqrt{x^2 - y^2}} \cdot \left(-\frac{1}{x^2} \right) = -\frac{y}{x \sqrt{x^2 - y^2}}$

Аналогично

$z_y' = \left( \arcsin \frac{y}{x} \right)'_y = \frac{1}{\sqrt{1 - \left( \frac{y}{x} \right)^2}} \cdot \left( \frac{y}{x} \right)'_y = \frac{x}{\sqrt{x^2 - y^2}} \cdot \frac{1}{x} \cdot (y)'_y = \frac{1}{\sqrt{x^2 - y^2}}$

Ответ

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Частные производные первого порядка

Примеры вычисления частных производных первого порядка