Производная второго порядка

ОПРЕДЕЛЕНИЕ

Рассмотрим дифференцируемую на 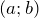$(a;b)$ функцию 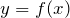$y = f(x)$ . Ее производная 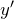$y'$ также является функцией аргумента 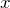$x$ . Если эту функцию продифференцировать еще раз, то получим вторую производную функции $y = f(x)$ :

$y'' = (y')'$

Итак, производная второго порядка есть первая производная от производной первого порядка.

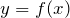ПРИМЕР 1

Задание

Найти производную второго порядка функции $y = x^3 - 4x + 13$

Решение

Для того чтобы найти вторую производную, вначале надо найти производную первого порядка:

$y' = \left( x^3 - 4x + 13 \right)'$

Согласно свойству линейности, имеем:

$y' = \left( x^3 \right)' - 4 \cdot (x)' + (13)' = 3x^2 - 4 \cdot 1 + 0 = 3x^2 - 4$

Тогда искомая вторая производная

$y'' = \left(y' \right)' = \left( 3x^2 - 4 \right)' = 3 \cdot \left( x^2 \right)' - (4)' = 3 \cdot 2x - 0 = 6x$

Ответ

$y'' = 6x$

ПРИМЕР 2

Задание

Найти вторую производную функции $y = x \cos x .$

Решение

Продифференцируем заданную функцию:

$y' = (x \cos x)'$

Согласно правилу дифференцирования произведения, имеем:

$y' = (x)' \cdot \cos x + x \cdot (\cos x)' = 1 \cdot \cos x + x \cdot (- \sin x) = \cos x - x \sin x$

После второго дифференцирования получаем:

$y'' = (y')' = (\cos x - x \sin x)' = (\cos x)' - (x \sin x)' = - \sin x - \left( (x)' \cdot \sin x + x \cdot (\sin x)' \right) =$

$= - \sin x - (1 \cdot \sin x + x \cdot \cos x) = -\sin x - \sin x - x \cos x = -2 \sin x - x \cos x$

Ответ

$y'' = -2 \sin x - x \cos x$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Производная второго порядка