Формула Тейлора для разложения функции

ОПРЕДЕЛЕНИЕ

Формулой Тейлора или рядом Тейлора в окрестности точки $x=a$ называется выражение вида

$f\left( x \right)=f\left( a \right)+\frac{{f}'\left( a \right)}{1!}\left( x-a \right)+\frac{{f}''\left( a \right)}{2!}{{\left( x-a \right)}^{2}}+\frac{{f}'''\left( a \right)}{3!}{{\left( x-a \right)}^{3}}+...+\frac{{{f}^{\left( n \right)}}\left( a \right)}{n!}{{\left( x-a \right)}^{n}}+...=$

$=\sum\limits_{n=0}^{\infty }{\frac{{{f}^{\left( n \right)}}\left( a \right)}{n!}{{\left( x-a \right)}^{n}}}$

Формула Тейлора в окрестности точки $x=0$ называется формулой Маклорена.

Ряды Маклорена для некоторых элементарных функций:

ПРИМЕР 1

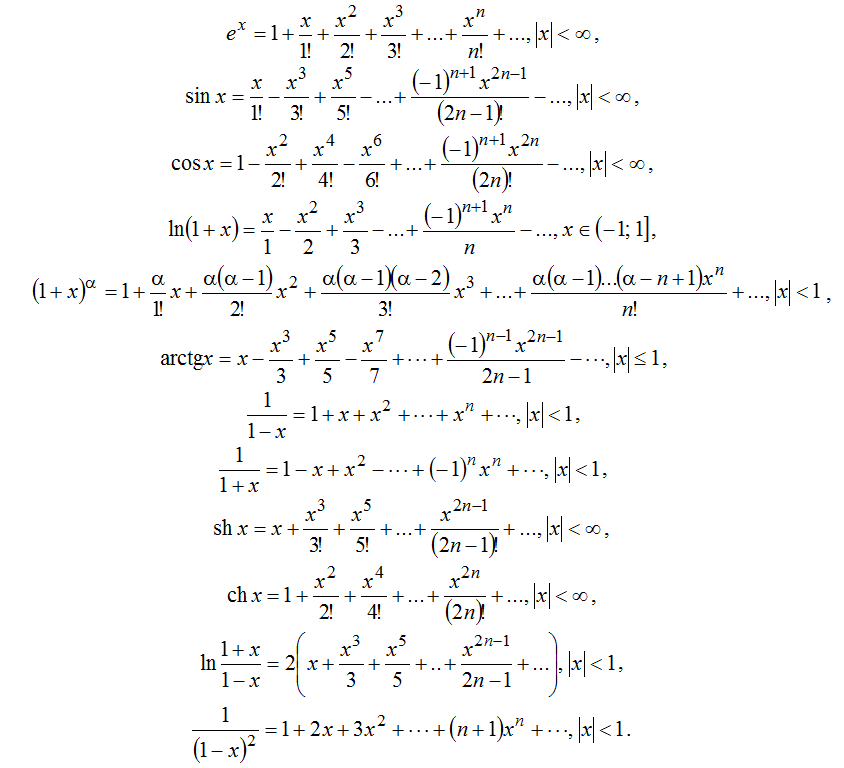
Задание

Вычислить приближенно $\ln 7 ,$ записав четыре первых члена его разложения в ряд Маклорена.

Решение

Для вычисления используем разложение

$\ln \frac{1+x}{1-x}=2\left( x+\frac{{{x}^{3}}}{3}+\frac{{{x}^{5}}}{5}+..+\frac{{{x}^{2n-1}}}{2n-1} \right),\ \left| x \right|<1$

Из равенства $7=\frac{1+x}{1-x}$ находим $x :$

$x=\frac{3}{4}$

Таким образом,

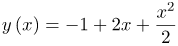$\ln 7=\ln \frac{1+\frac{3}{4}}{1-\frac{3}{4}}=2\cdot \left( \frac{3}{4}+\frac{{{\left( \frac{3}{4} \right)}^{3}}}{3}+\frac{{{\left( \frac{3}{4} \right)}^{5}}}{5}+\frac{{{\left( \frac{3}{4} \right)}^{7}}}{7}+... \right)\approx$