Формула напряжённости магнитного поля
![Rendered by QuickLaTeX.com \[ H = \frac{B}{\mu_{0}} - M \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-61fc678958f98ad9f439e47357b1cd6c_l3.png)
Здесь ![]() – напряжённость магнитного поля,
– напряжённость магнитного поля, ![]() – магнитная индукция,
– магнитная индукция, ![]() – магнитная постоянная,
– магнитная постоянная, ![]() — намагниченность.
— намагниченность.
Единица измерения напряжённости магнитного поля – А/м (ампер на метр).
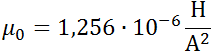
Напряжённость – векторная величина, характеризующая интенсивность воздействия магнитного поля на намагниченную заряжённую частицу (пробный магнит) в конкретной точке. В векторной форме уравнение выглядит так:
![Rendered by QuickLaTeX.com \[ \overline{H} = \frac{\overline{B}}{\mu_{0}} - \overline{M} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-88c49b8ea3f153629908f724e079cd91_l3.png)
Примеры решения задач по теме «Напряжённость магнитного поля»
| Задание | Найти напряжённость магнитного поля в точке, в которой магнитная индукция равна 9 Тл, а намагниченность 7 мА/м. |
| Решение | Переведём кА в А : 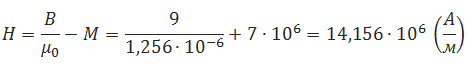
|
| Ответ | Напряжённость магнитного поля равна |
| Задание | Катушка создаёт внутри себя однородное магнитное поле напряжённостью H. Вектор 
|
| Решение | В векторном виде формула напряжённости поля выглядит так:
Если рассмотреть плоскость Аналогичные рассуждения верны и для |
| Ответ | 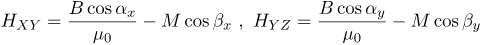 |











