Формула индукции магнитного поля

ОПРЕДЕЛЕНИЕ

Векторной характеристикой магнитного поля является вектор магнитной индукции. Его обозначают как: $\overline{B}$ .

Направлением вектора магнитной индукции считают направление на север магнитной стрелки, которая может свободно вращаться в магнитном поле. Такое же направление имеет положительная нормаль к замкнутому контуру, по которому течет ток. Положительная нормаль имеет направление, совпадающее с направлением перемещения правого винта (буравчика), если его вращают по направлению тока в контуре.

Модуль вектора магнитной индукции можно установить, используя силу, которая действует на проводники с током, помещенные в магнитное поле (силу Ампера). Тогда модуль вектора $\overline{B}$ равен частному от деления максимальной силы ( $F_{max}$ ), с которой магнитное поле оказывает воздействие на отрезок проводника с током (I) к произведению силы тока на длину проводника ( $\Delta l$ ):

$B=\frac{F_{max}}{I\Delta l} \qquad(1)$

Рассматривая силу Лоренца, которая действует на заряженную частицу, движущуюся в магнитном поле, получают формулу для магнитной индукции в виде:

$B=\frac{F_L}{qv\sin \alpha \ } } \qquad(2)$

где $F_L$ – модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле; $\alpha$ – это угол между векторами $\overline{v}$ и $\overline{B}$ . Направления ${\overline{F}}_L$ , векторов $\overline{v}$ и $\overline{B}$ связаны между собой правилом левой руки.

Формулой, которая определяет величину вектора магнитной индукции в данной точке магнитного поля, считают так же следующее выражение:

$B=\frac{M_{max}}{p_m} \qquad(3)$

где $M_{max}$ – максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом $p_m$ , равным единице, если нормаль к рамке перпендикулярна направлению поля. Вращающий момент (M), действующий на контур с током I в однородном магнитном поле можно вычислить как:

$M=BIS{\sin \alpha } \qquad(4)$

где S – площадь, которую обтекает ток I. Следует помнить, что максимальный вращающий момент получается тогда, когда плоскость контура параллельна линиям магнитной индукции поля ( ${\sin \alpha } =1$ ).

Принцип суперпозиции магнитных полей

Если магнитное поле получается в результат наложения нескольких магнитных полей то, магнитная индукция поля ( $\overline{B}$ ), может быть найдена как векторная сумма магнитных индукций отдельных полей ( ${\overline{B}}_i$ ):

$\overline{B}=\sum^N_{i=1}{{\overline{B}}_i}\ \qquad(5)$

Закон Био-Савара-Лапласа, как формула для вычисления величины индукции магнитного поля

Закон Био-Савара – Лапласа является одним из распространенных законов, который позволяет вычислить вектор магнитной индукции ( $d\overline{B}$ ) в любой точке магнитного поля, создаваемого в вакууме элементарным проводником с током:

$d\overline{B}=\frac{{\mu }_0}{4\pi }\frac{I}{r^3}\left[d\overline{l}\overline{r}\right]\ \qquad(6)$

где I – сила тока; $d\overline{l}$ – вектор элементарный проводник по модулю он равен длине проводника, при этом его направление совпадает с направлением течения тока; $\overline{r}$ – радиус-вектор, который проводят от элементарного проводника к точке, в которой находят поле; ${\mu }_0=4\pi \cdot {10}^{-7}\frac{Гн}{м}$ – магнитная постоянная. Вектор $d\overline{B}$ является перпендикулярным к плоскости, в которой расположены $d\overline{l}$ и $\overline{r}$ , конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта).

Для однородного и изотропного магнетика, заполняющего пространство, вектор магнитной индукции в вакууме( ${\overline{B}}_0)$ и в веществе ( $\overline{B}$ ), при одинаковых условиях, связывает формула:

$\overline{B}=\mu {\overline{B}}_0\ \qquad(7)$

где $\mu$ – относительная магнитная проницаемость вещества.

Частные случаи формул для вычисления модуля вектора магнитной индукции

Формула для вычисления модуля вектора индукции в центре кругового витка с током (I):

$B=\frac{{\mu }_0\mu }{2}\frac{I}{R} \qquad(8)$

где R – радиус витка.

Модуль вектора магнитной индукции поля, которое создает бесконечно длинный прямой проводник с током:

$B=\frac{{\mu }_0\mu }{2\pi }\frac{I}{r} \qquad(9)$

где r – расстояние от оси проводника до точки, в которой рассматривается поле.

В средней части соленоида магнитная индукция поля вычисляется при помощи формулы:

$B={\mu }_0\mu nI\ \left(10\right)$

где n – количество витков соленоида на единицу длины; I – сила тока в витке.

Примеры решения задач по теме «Индукция магнитного поля»

ПРИМЕР 1

Задание

Какой максимальный вращающий момент может действовать на катушку с током в 2 А? Если магнитное поле в котором находится катушка является однородным $B=0,05$ Тл. Катушка плоская и прямоугольная, имеет N=200 витков. Стороны витков $a=0,1$ м и $b=0,05$ м.

Решение

В качестве основы для решения задачи используем формулу, которая определяет, что максимальный вращающий момент ( $M_{max}$ ), действующий на контур с током I в однородном магнитном поле можно вычислить как:

$M_{max}=BIS \qquad(1.1)$

Так как у нас имеется катушка с N витками, формулу (1.1) преобразуем к виду:

${M'}_{max}=NBIS=NBIab \qquad(1.2)$

где $S=a\cdot b$ .

Вычислим ${M'}_{max}$ :

${M'}_{max}=200\cdot 0,05\cdot 2\cdot 0,1\cdot 0,05=0,1\ \left(H\cdot m\right)$

Ответ

${M'}_{max}=0,1 H\cdot$ м

ПРИМЕР 2

Задание

Какой должна быть величина индукции магнитного поля (B) для того, чтобы сила Ампера могла уравновесить силу тяжести проводника, находящегося в магнитном поле горизонтально? Масса проводника m, длина $l,$ сила тока, текущая по проводнику $I.$ Покажите на рисунке как должно быть направлен вектор магнитного поля ( $\overline{B}$ )?

Решение

Сделаем рисунок.

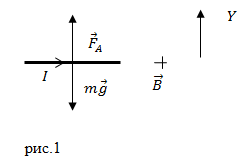
Определим для начала направление вектора индукции магнитного поля. Для этого следует использовать правило левой руки в определении направлений связывающих векторы силу Ампера, вектор магнитной индукции и направление течения тока. Оттолкнемся от того, что сила Ампера должна быть направлена по одной прямой с силой тяжести и быть противоположно ей направленной для того, чтобы стержень был в равновесии. Отогнутый на $90^\circ$ большой палец по силе Ампера (рис.1), четыре пальца по току, линии поля входят в ладонь. Получается, что вектор индукции будет перпендикулярен плоскости рисунка и направлен от нас.