Формула вектора магнитной индукции
Направление вектора магнитной индукции
Направлением вектора магнитной индукции считают направление, которое показывает северный полюс магнитной стрелки, которая может свободно устанавливаться в магнитном поле. Аналогичное направление имеет положительная нормаль к замкнутому контуру, по которому течет ток. Положительная нормаль имеет направление, совпадающее с направлением перемещения правого винта (буравчика), если его вращают по направлению тока в контуре. При использовании рамки с током или магнитной стрелки можно определить направление вектора ![]() в любой точке магнитного поля.
в любой точке магнитного поля.
Если магнитное поле создает прямой проводник с током, то магнитная стрелка в любой точке этого поля устанавливается по касательной к окружности, плоскость которой перпендикулярна проводнику, центр находится на оси провода. Направление вектора ![]() определяют при помощи правила правого винта (правила буравчика), которое говорит о том, что если поступательное перемещение буравчика совпадает с направлением течения тока в проводнике, то вращение головки винта совпадает с направлением вектора магнитной индукции.
определяют при помощи правила правого винта (правила буравчика), которое говорит о том, что если поступательное перемещение буравчика совпадает с направлением течения тока в проводнике, то вращение головки винта совпадает с направлением вектора магнитной индукции.
Величина (модуль) вектора магнитной индукции
Магнитное поле оказывать действие на каждый участок проводника с током. Используя силу, действующую на проводник с током (силу Ампера), определяют величину вектора магнитной индукции магнитного поля. Так, модуль вектора ![]() равен частному от деления максимальной силы Ампера
равен частному от деления максимальной силы Ампера ![]() , с которой магнитное поле оказывает воздействие на отрезок проводника с током (I) к произведению силы тока на длину проводника
, с которой магнитное поле оказывает воздействие на отрезок проводника с током (I) к произведению силы тока на длину проводника ![]() :
:
![]()
На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца. По величине ее воздействия на заряд также можно установить модуль вектора ![]() :
:
![]()
где ![]() – модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле;
– модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле; ![]() – это угол между векторами
– это угол между векторами ![]() и
и ![]() . Направления
. Направления ![]() , векторов
, векторов ![]() и
и ![]() связаны между собой правилом левой руки.
связаны между собой правилом левой руки.
Формулой, которая определяет величину вектора магнитной индукции в конкретной точке магнитного поля можно считать следующее выражение:
![]()
где ![]() – максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом
– максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом ![]() , равным единице, если нормаль к рамке перпендикулярна направлению поля.
, равным единице, если нормаль к рамке перпендикулярна направлению поля.
Основные формулы, которые служат для вычисления вектора магнитной индукции
Закон Био-Савара-Лапласа
Данный закон предоставляет нам возможность вычислить вектор магнитной индукции (![]() ) в любой точке магнитного поля, которое создается в вакууме элементарным проводником с током:
) в любой точке магнитного поля, которое создается в вакууме элементарным проводником с током:
![]()
где I – сила тока; ![]() – вектор элементарный проводник по модулю он равен длине проводника, при этом его направление совпадает с направлением течения тока;
– вектор элементарный проводник по модулю он равен длине проводника, при этом его направление совпадает с направлением течения тока; ![]() – радиус-вектор, который проводят от элементарного проводника к точке, в которой находят поле;
– радиус-вектор, который проводят от элементарного проводника к точке, в которой находят поле; ![]() – магнитная постоянная. Вектор
– магнитная постоянная. Вектор ![]() является перпендикулярным к плоскости, в которой расположены
является перпендикулярным к плоскости, в которой расположены ![]() и
и ![]() , конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта).
, конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта).
Для однородного и изотропного магнетика, заполняющего пространство, вектор магнитной индукции в вакууме(![]() ) и в веществе (
) и в веществе (![]() ), при одинаковых условиях, связывает формула:
), при одинаковых условиях, связывает формула:
![]()
где ![]() – относительная магнитная проницаемость вещества.
– относительная магнитная проницаемость вещества.
Принцип суперпозиции
Магнитная индукция поля (![]() ), которое является наложением нескольких полей, находится как векторная сумма магнитных индукций отдельных полей (
), которое является наложением нескольких полей, находится как векторная сумма магнитных индукций отдельных полей (![]() ):
):
![Rendered by QuickLaTeX.com \[\overline{B}=\sum^N_{i=1}{{\overline{B}}_i}\ \qquad(6)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f451f154356638ca271a1bcb15059d17_l3.png)
Теорема о циркуляции
В однородном и изотропном веществе циркуляция вектора индукции магнитного поля по любому контуру L равна:
![Rendered by QuickLaTeX.com \[\oint_L{\overline{B}d\overline{l}=\mu {\mu }_0\sum^N_{k=1}{I_k}} \qquad (7)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1872d56fa88e9d0876c1116e8b684e63_l3.png)
где ![]() – сумма токов проводимости с учетом их знака, которые охвачены рассматриваемым контуром;
– сумма токов проводимости с учетом их знака, которые охвачены рассматриваемым контуром; ![]() – магнитная проницаемость вещества. В том случае, если направление обхода контура связано с направлением течения тока при помощи правила правого винта, то ток считают положительным.
– магнитная проницаемость вещества. В том случае, если направление обхода контура связано с направлением течения тока при помощи правила правого винта, то ток считают положительным.
В случае непрерывного распределения тока по поверхности S силу тока вычисляют при помощи выражения:
![]()
где ![]() равен по модулю площади элемента поверхности
равен по модулю площади элемента поверхности ![]() – плотность тока.
– плотность тока.
Примеры частных случаев формул для нахождения вектора магнитной индукции см. раздел «Магнитная индукция формула»
Примеры решения задач по теме «Вектор магнитной индукции»
| Задание | Используя теорему о циркуляции вектора магнитной индукции, определите величину вектора |
| Решение | Сделаем рисунок.
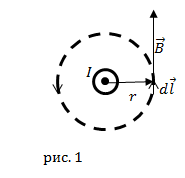
На рис. 1 проводник, по которому течет ток, перпендикулярен плоскости рисунка. Ток течет на нас, проводник с током изображен точкой. В качестве контура, по которому будем рассматривать циркуляцию вектора где Величина где Выразим величину вектора магнитной индукции из (1.4): |
| Ответ | |
| Задание | Два длинных параллельных проводника с токами I создают магнитное поле. Расстояние между проводниками равно d. Токи текут в противоположных направлениях. Какова величина магнитной индукции в точке, которая находится на расстоянии |
| Решение | Сделаем рисунок.
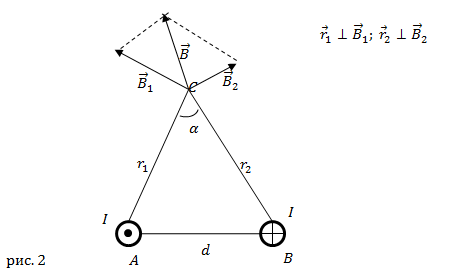
Используем результат примера 1, запишем, что: Из принципа суперпозиции, в рассматриваемой точке имеем: По теореме косинусов: Из треугольника ABC рис. 1 имеем: Получаем: |
| Ответ | |






![Rendered by QuickLaTeX.com \[\oint_L{\overline{B}d\overline{l}=\mu {\mu }_0\sum^N_{k=1}{I_k}} \qquad (1.1)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e95e08836728c7b0f9bfb342200ed4e4_l3.png)
![Rendered by QuickLaTeX.com \[\sum^N_{k=1}{I_k}=I\ \qquad(1.2)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d2313db3fddf3af69e9642eee9a2a5cd_l3.png)
![Rendered by QuickLaTeX.com \[B=\frac{{\mu }_0}{2\pi }I\sqrt{\frac{1}{r^2_1}+\frac{1}{r^2_2}-\frac{1}{r^2_1r^2_2}(r^2_1+r^2_2-d^2)}=\frac{{\mu }_0}{2\pi }I\frac{d}{r_1r_2}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-c52868a1b6196e5f5e98b9ffc217ebe4_l3.png)





