Формула магнитной индукции

ОПРЕДЕЛЕНИЕ

Одной из основных количественных характеристик магнитного поля является вектор магнитной индукции ( $\overline{B}$ ).

Формулы определяющие величину вектора магнитной индукции получают, используя выражение для силы Ампера, силы Лоренца и применяя понятие вращающего момента.

Формула величины вектора магнитной индукции

Формулой, которая определяет величину вектора магнитной индукции в конкретной точке магнитного поля можно считать следующее выражение:

$B=\frac{M_{max}}{p_m} \qquad(1)$

где $M_{max}$ – максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом $p_m$ , равным единице, если нормаль к рамке перпендикулярна направлению поля.

При помощи силы Ампера величина вектора магнитной индукции задана как:

$B=\frac{1}{I}{\left(\frac{dF}{dl}\right)}_{max} \qquad(2)$

где модуль $\overline{B}$ равен пределу отношения величины силы ( $dF$ ), с которой магнитное поле действует на бесконечно малый проводник с током, к силе тока (I) умноженной на длину этого проводника ( $dl$ ), если длина проводника стремится к нулю. Как известно кроме величины вектор магнитной индукции имеет направление. В данном случае $\overline{B}$ перпендикулярен к направлению силы $dF$ и перпендикулярен направлению элемента проводника. Если рассматривать вращение из конца вектора магнитной индукции по кратчайшему расстоянию от направления силы к направлению тока, оно должно идти против часовой стрелки.

Используя силу Лоренца, получают формулу для магнитной индукции в виде:

$B=\frac{F_L}{qv\sin \alpha \ } } \qquad(3)$

где $F_L$ – модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле; $\alpha$ – это угол между векторами $\overline{v}$ и $\overline{B}$ . Направления ${\overline{F}}_L$ , векторов $\overline{v}$ и $\overline{B}$ связаны между собой правилом левой руки.

Закон Био-Савара-Лапласа

Данный закон предоставляет нам возможность вычислить вектор магнитной индукции ( $d\overline{B}$ ) в любой точке магнитного поля, которое создается в вакууме элементарным проводником с током:

$d\overline{B}=\frac{{\mu }_0}{4\pi }\frac{I}{r^3}\left[d\overline{l}\overline{r}\right]\ \qquad(4)$

где I – сила тока; $d\overline{l}$ – вектор элементарный проводник по модулю он равен длине проводника, при этом его направление совпадает с направлением течения тока; $\overline{r}$ – радиус-вектор, который проводят от элементарного проводника к точке, в которой находят поле; ${\mu }_0=4\pi \cdot {10}^{-7}\frac{Гн}{м}$ – магнитная постоянная. Вектор $d\overline{B}$ является перпендикулярным к плоскости, в которой расположены $d\overline{l}$ и $\overline{r}$ , конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта).

Для однородного и изотропного магнетика, заполняющего пространство, вектор магнитной индукции в вакууме( ${\overline{B}}_0)$ и в веществе ( $\overline{B}$ ), при одинаковых условиях, связывает формула:

$\overline{B}=\mu {\overline{B}}_0\ \qquad(5)$

где $\mu$ – относительная магнитная проницаемость вещества.

Частные случаи формул для вычисления величины вектора магнитной индукции

Формула для вычисления модуля вектора индукции в центре кругового витка с током (I):

$B=\frac{{\mu }_0\mu }{2}\frac{I}{R} \qquad(6)$

где R – радиус витка.

Модуль вектора магнитной индукции поля, которое создает бесконечно длинный прямой проводник с током:

$B=\frac{{\mu }_0\mu }{2\pi }\frac{I}{r} \qquad(7)$

где r – расстояние от оси проводника до точки, в которой рассматривается поле.

В средней части соленоида магнитная индукция поля вычисляется при помощи формулы:

$B={\mu }_0\mu nI\ \qquad(8)$

где n – количество витков соленоида на единицу длины; I – сила тока в витке.

Принцип суперпозиции

Магнитная индукция поля ( $\overline{B}$ ), которое является наложением нескольких полей, находится как векторная сумма магнитных индукций отдельных полей ( ${\overline{B}}_i$ ):

$\overline{B}=\sum^N_{i=1}{{\overline{B}}_i}\ \qquad(9)$

Примеры решения задач по теме «Магнитная индукция»

ПРИМЕР 1

Задание

Какова магнитная индукция поля в вакууме, которую создают два тока в точке находящейся на равном расстоянии от каждого проводника (рис.1)? Проводники являются бесконечно длинными, прямыми. Расстояние между ними равно r. Провода параллельные, текущие в них токи равны I, они имеют одинаковые направления.

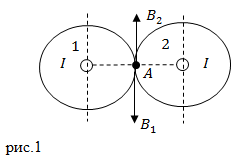
Решение

В соответствии с принципом суперпозиции результирующая индукция магнитного поля должна быть найдена как векторная сумма:

$\overline{B}={\overline{B}}_1+{\overline{B}}_2 \qquad(1.1)$

где ${\overline{B}}_1$ – индукция, которую создает первый ток; ${\overline{B}}_2$ – индукция, которую создает второй ток. Из рис. 1 видно, что векторы ${\overline{B}}_1$ и ${\overline{B}}_2$ направлены вдоль одной прямой , но в разные стороны, следовательно:

$B=B_1-B_2\ \qquad(1.2)$

Величину вектора магнитной индукции в точке А поля, которое создает первый проводник можно найти используя формулу:

$B_1=\frac{{mi}_0\mu }{2\pi }\frac{I}{r_1} \qquad(1.3)$

где $r_1=\frac{r}{2}$ ; $\mu =1$ . Второй проводник в точке А создает точно такую же по величине магнитную индукцию:

$B_2=\frac{{\mu }_0\mu }{2\pi }\frac{I}{r_2} \qquad(1.4)$

$r_2=\frac{r}{2}$ . Получаем, что в точке А:

$B_1=B_2\ \to B=B_1-B_2=0$

Ответ

$B=0$

ПРИМЕР 2

Задание

Какова магнитная индукция в центре тонкого кольца, находящегося в вакууме, если по нему течет ток, равный $I=10$ А? Радиус кольца равен $R=0,05$ м.

Решение

В качестве основы для решения задачи используем закон Био-Савара-Лапласа для вакуума. Выделим на круговом токе элементарный участок, который можно считать прямолинейным. В центре окружности этот участок создает поле равное:

$dB=\frac{{\mu }_0}{4\pi }\frac{Idl}{R^2}\ \qquad(2.1)$

Все векторы магнитной индукции от всех элементов тока при движении по окружности будут направлены вдоль одной прямой, поэтому векторное суммирование заменим простым интегрированием:

$B=\int_L{\frac{{\mu }_0}{4\pi }\frac{Idl}{R^2}}=\frac{{\mu }_0}{4\pi }\frac{I2\pi R}{R^2}=\frac{{\mu }_0}{2R}I\$