Точка пересечения биссектрис треугольника
Определение и точка пересечения биссектрис треугольника
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.
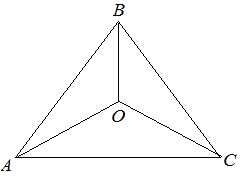
Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилегающим сторонам:
Первая замечательная точка треугольника – точка пересечения биссектрис. Точка пересечения биссектрис является центром вписанной в треугольник окружности и всегда находится внутри треугольника.
Примеры решения задач
| Задание | В треугольнике 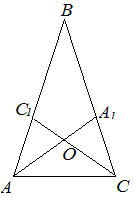
|
| Решение | Поскольку Так как Из треугольника |
| Ответ |
| Задание | В треугольнике 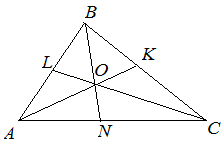
|
| Решение | Рассмотрим треугольник откуда Тогда периметр треугольника |
| Ответ |











