Биссектриса в равнобедренном треугольнике

Определение и формулы биссектрисы равнобедренного треугольника

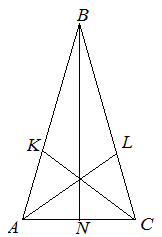
В равнобедренном треугольнике биссектриса угла, лежащего против основания, является медианой и высотой.

Три биссектрисы равнобедренного треугольника пересекаются в одной точке, называемой инцентром треугольника.

Для биссектрисы равнобедренного треугольника справедливы следующие утверждения:

• Биссектрисы делят противоположные боковые стороны треугольника на части, пропорциональные прилегающим сторонам:

   

• Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в этот треугольник.
• Биссектриса угла – это геометрическое место точек, равноудаленных от сторон этого угла.
• Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.

Примеры решения задач

ПРИМЕР 1

Задание	В равнобедренном треугольнике 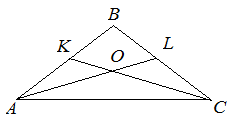провели биссектрисы и , которые пересекаются в точке . Найти угол , если .
Решение	Поскольку треугольник равнобедренный, то углы при основании равны:     Рассмотрим треугольник . Так как и – биссектрисы углов и соответственно, то     Тогда, согласно теореме про сумму углов треугольника,
Ответ

ПРИМЕР 2

Задание	В равнобедренном треугольнике 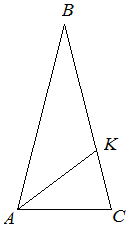с боковой стороной см и основанием см провели биссектрису . Найти длины отрезков и .
Решение	В равнобедренном треугольнике боковые стороны равны, а значит     Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам, т.е.     Пусть , тогда , отсюда     Таким образом,     Получили, что см, а см.
Ответ	см, см