Медиана в равнобедренном треугольнике

Определение и формулы медианы равнобедренного треугольника

ОПРЕДЕЛЕНИЕ

Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны этого треугольника.

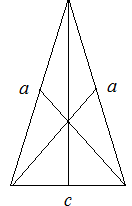
В равнобедренном треугольнике медиана, опущенная на основание, является высотой и биссектрисой.

Для медиан равнобедренного треугольника справедливы следующие утверждения:

Медианы равнобедренного треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
Медиана разбивает равнобедренный треугольник на два треугольника с одинаковой площадью.
Весь равнобедренный треугольник делится своими медианами на шесть равновеликих (т.е. с одинаковой площадью) треугольников.

Медиана равнобедренного треугольника, проведенная к его основанию, вычисляется по формуле:

$m_{c} =\frac{1}{2} \sqrt{4a^{2} -c^{2}} ,$

где $c$ – основание равнобедренного треугольника, $a$ – боковые стороны треугольника.

Примеры решения задач

ПРИМЕР 1

Задание

В равнобедренном треугольнике $ABC$ боковая сторона $AB=4$ см и угол при основании равен $75^{\circ}$ . Найти медиану, проведенную к стороне $BC$ .

Пример 1, медиана в равнобедренном треугольнике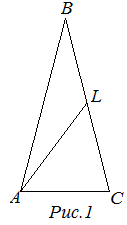

Решение

Рассмотрим равнобедренный треугольник $ABC$ (рис. 1), в котором

$AB=BC=4 cm$

$\angle A=\angle C=75^{\circ}$

Тогда

$\angle B=180^{\circ} -75^{\circ} -75^{\circ} =30^{\circ}$

Проведем медиану $AL$ к стороне $BC$ , которая разделит ее на равные отрезки

$BL=LC=2cm$

Рассмотрим треугольник $ABL$ и, пользуясь теоремой косинусов, найдем $AL$ :

$AL^{2} =AB^{2} +BL^{2} -2\cdot AB\cdot BL\cdot \cos B=$

$=16+4-2\cdot 4\cdot 2\cdot \frac{\sqrt{3}}{2} =20-8\sqrt{3} =4(5-2\sqrt{3} )$

тогда

$AL=2\sqrt{5-2\sqrt{3}} cm$

Ответ

$AL=2\sqrt{5-2\sqrt{3}}$ см

ПРИМЕР 2

Задание

В равнобедренном треугольнике 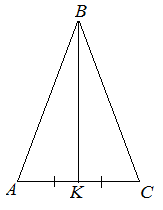$ABC$ боковая сторона на 1 см меньше основания, а медиана, проведенная к основанию, равна 4 см. Найти площадь треугольника $ABC$ .

Пример 2, медиана в равнобедренном треугольнике

Решение

В равнобедренном треугольнике $ABC$ проведем медиану $BK=4$ см к основанию $AC$ . Пусть $AC=x$ см, тогда $AB=(x-1)$ см, а $AK=\frac{x}{2}$ см. Поскольку треугольник $ABC$ равнобедренный, то медиана $BK$ является и высотой. Следовательно, треугольник $ABK$ – прямоугольный. Запишем для него теорему Пифагора:

$AB^{2} =AK^{2} +BK^{2}$