Биссектриса в прямоугольном треугольнике

Определение и формулы биссектрисы в прямоугольном треугольнике

ОПРЕДЕЛЕНИЕ

Биссектриса угла треугольника – это луч, который исходит из вершины треугольника, и делит данный угол пополам.

Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.

Биссектриса угла – это геометрическое место точек, равноудаленных от сторон этого угла.

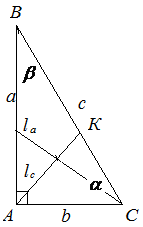
Биссектриса в прямоугольном треугольнике

Биссектриса делит противоположную сторону треугольника на части, пропорциональные прилегающим сторонам:

$\frac{AB}{AC} =\frac{BK}{KC}$

Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в этот треугольник.

Рассмотрим прямоугольный треугольник с катетами $a$ и $b$ , гипотенузой $c$ , острыми углами $\alpha$ и $\beta$ . Проведем биссектрису прямого угла $l_{c}$ . Ее длина выражается через длины катетов следующим образом:

$l_{c} =\sqrt{2} \frac{ab}{a+b}$

Проведем биссектрису $l_{a}$ острого угла $\alpha$ , тогда

$l_{a} =\frac{b}{\cos(\alpha / 2)}$

или

$l_{a} =b\cdot \sqrt{\frac{2c}{b+c}}$

Примеры решения задач

ПРИМЕР 1

Задание

В прямоугольном треугольнике с катетами $a=6$ см и $b=8$ см найти длину биссектрисы, проведенной к стороне $a$ .

Решение

Найдем длину гипотенузы $c$ . По теореме Пифагора

$c=\sqrt{a^{2} +b^{2}} =\sqrt{36+64} =10cm$

Длину биссектрисы, проведенной к стороне $a$ , вычислим по формуле:

$l_{a} =b\cdot \sqrt{\frac{2c}{b+c}} =8\cdot \sqrt{\frac{2\cdot 10}{8+10}} =\frac{8\sqrt{10}}{3} cm$

Ответ

$l_{a} =\frac{8\sqrt{10}}{3}$ см

ПРИМЕР 2

Задание

Биссектриса прямого угла треугольника $ABC$ делит гипотенузу на отрезки $30$ см и $40$ см. Найти периметр этого треугольника.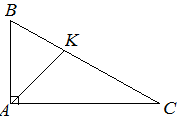

Решение

Рассмотрим прямоугольный треугольник $ABC$ и проведем биссектрису $BK$ . По условию задачи $BK=30$ см и $KC=40$ см. Поскольку биссектриса делит противоположную сторону треугольника на части, пропорциональные прилегающим сторонам, то

$\frac{BK}{KC} =\frac{AB}{AC} =\frac{30}{40} =\frac{3}{4}$