Точка пересечения высот треугольника
Определение и точка пересечения высот треугольника
Из каждой вершины треугольника можно опустить высоту.
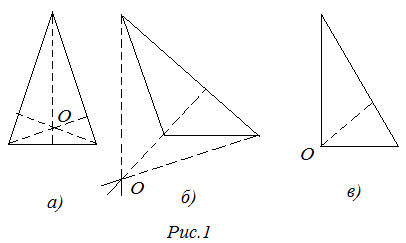
Три высоты в треугольнике пересекаются в одной точке и эту точку называют ортоцентром треугольника.
Если треугольник остроугольный, то точка пересечения высот лежит внутри треугольника (рис. 1, а), если тупоугольный – то вне треугольника (рис. 1, б), в прямоугольном треугольнике эта точка находится в вершине прямого угла (рис. 1, в).
Примеры решения задач
| Задание | В треугольнике с углами 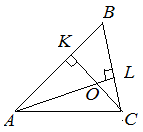
|
| Решение | Рассмотрим треугольник а из прямоугольного треугольника Тогда из треугольника |
| Ответ |
| Задание | В треугольнике 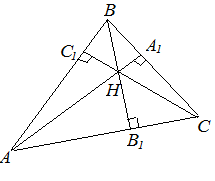
|
| Доказательство | Рассмотрим треугольник Рассмотрим треугольник Из четырехугольника Поскольку Аналогично доказывается равенство остальных радиусов. Что и требовалось доказать. |











