Точка пересечения медиан треугольника

Определение и точка пересечения медиан треугольника

ОПРЕДЕЛЕНИЕ

Медианой треугольника называется отрезок, соединяющий вершину треугольника и середину противоположной стороны.

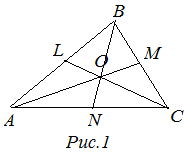
Из каждой вершины треугольника можно опустить медиану.

Три медианы в треугольнике пересекаются в одной точке и эту точку называют центром тяжести треугольника.

Точка пересечения медиан делит каждую медиану в отношении $2:1$ , считая от вершины.

Отрезки прямых, соединяющих вершины треугольника с центром тяжести, делят треугольник на три равновеликих треугольника (т.е. на треугольники с одинаковой площадью).

Примеры решения задач

ПРИМЕР 1

Задание

В треугольнике 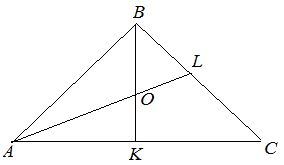$ABC$ медианы $AL=BK=6$ см пересекаются в точке $O$ . Найти угол $AOK$ , если $AC=8$ см.

Пример 1, точка пересечения медиан треугольника

Решение

Поскольку медианы точкой пересечения делятся в отношении $2:1$ , то можно найти длины отрезков

$AO=4$ см и $OK=2$ см,

$AK=\frac{1}{2} AC=4 cm$

Рассмотрим треугольник $AOK$ и запишем теорему косинусов для стороны $AK$ :

$AK^{2} =AO^{2} +OK^{2} -2\cdot AO \cdot OK \cdot \cos \angle AOK;$

и выразим

$\cos \angle AOK=\frac{AK^{2} -AO^{2} -OK^{2}}{-2\cdot AO\cdot OK} =\frac{16-16-4}{-2\cdot 4\cdot 2} =\frac{1}{4}$

Тогда $\angle AOK=\arccos \frac{1}{4}$ .

Ответ

$\angle AOK=\arccos \frac{1}{4}$

ПРИМЕР 2

Задание

Найти координаты точки пересечения медиан треугольника с вершинами $A(1,2),\ B(2,3)$ и $C(3,2)$ .

Решение

Рассмотрим треугольник $ABC$ (рис. 1). Найдем координаты середин сторон $AC$ и $AB$ соответственно:

$N\left(\frac{1+3}{2} ,\frac{2+2}{2} \right)\; \Rightarrow N(2,2),$

$L\left(\frac{1+2}{2} ,\frac{2+3}{2} \right)\; \Rightarrow L\left(1,5;2,5\right)$

Найдем уравнения медиан $CL$ и $BN$ как уравнения прямых, проходящих через две заданные точки:

$\left(CL\right):\frac{x-3}{1,5-3} =\frac{y-2}{2,5-2} \Rightarrow -1,5(y-2)=0,5(x-3)\Rightarrow y=-\frac{x}{3} +3$

$\left(BN\right):\frac{x-2}{2-2} =\frac{y-3}{2-3} \Rightarrow x=2$

Точка пересечения этих прямых будет иметь координаты $x=2$ и $y=-\frac{2}{3} +3=\frac{7}{3}$ , т.е. $O\left(2,\frac{7}{3} \right)$ .

Ответ

$O\left(2,\frac{7}{3} \right)$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Точка пересечения медиан треугольника

Определение и точка пересечения медиан треугольника

Примеры решения задач