Серединный перпендикуляр треугольника

Определение и формулы для расчета серединного перпендикуляра треугольника

ОПРЕДЕЛЕНИЕ

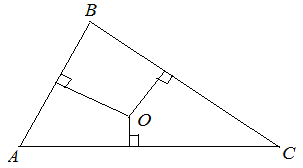
Серединный перпендикуляр треугольника – это перпендикуляр, проведенный к середине стороны треугольника.

Три срединных перпендикуляра треугольника пересекаются в одной точке, являющейся центром описанной окружности.

Точка пересечения серединных перпендикуляров в остроугольном треугольнике лежит внутри треугольника; в тупоугольном – вне треугольника; в прямоугольном – на середине гипотенузы.

Свойства срединных перпендикуляров треугольника:

Любая точка серединного перпендикуляра к стороне равноудалена от концов этой стороны.
Любая точка, равноудаленная от концов стороны, лежит на серединном перпендикуляре к ней.
Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.

Примеры решения задач

ПРИМЕР 1

Задание

В треугольнике 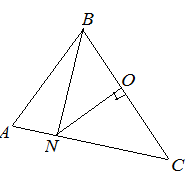$ABC$ серединный перпендикуляр к стороне $BC$ пересекает сторону $AC$ в точке $N$ . Найти $AN$ , если $BN=6$ см, а $AC=9$ см.

Пример 1, серединный перпендикуляр треугольника

Решение

Рассмотрим треугольник $ABC$ и проведем в нем серединный перпендикуляр $ON$ к стороне $BC$ . В треугольнике $BNC$ отрезок $ON$ является медианой и высотой, значит, этот треугольник является равнобедренным, т.е.

$BN=NC=6 cm$

Тогда

$AN=AC-NC=9-6=3 cm$

Ответ

$AN=3$ см

ПРИМЕР 2

Задание

В треугольнике 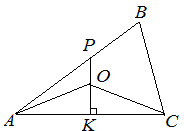$ABC$ из точки $K$ стороны $AC$ провели серединный перпендикуляр, который пересек сторону $AB$ в точке $P$ . На отрезке $PK$ взяли точку $O$ так, что $OK=3$ см. Найти периметр треугольника $AOC$ , если $AC=8$ см.

Пример 2, серединный перпендикуляр треугольника

Решение

В треугольнике $ABC$ отрезок $PK$ – серединный перпендикуляр, а значит

$AK=KC=\frac{1}{2} AC=4 cm$

По свойству серединного перпендикуляра точка $O$ равноудалена от концов стороны $AC$ , т.е. $AO=OC$ . Из прямоугольного треугольника $AKO$ по теореме Пифагора найдем $AO$ :