Пропорциональные отрезки в прямоугольном треугольнике

ОПРЕДЕЛЕНИЕ

Средним пропорциональным двух чисел $a$ и $b$ называется такое число $c$ , что

$c^{2} =ab$

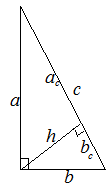
В прямоугольном треугольнике с катетами $a$ и $b$ высота $h$ , проведенная к гипотенузе $c$ , делит ее на отрезки $a_{c}$ и $b_{c}$ , которые называются проекциями катетов на гипотенузу.

Пропорциональные отрезки в прямоугольном треугольнике

Высота, опущенная из вершины прямого угла на гипотенузу, есть среднее пропорциональное между проекциями катетов:
$h^{2} =a_{c} \cdot b_{c}$
Каждый катет есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу:
$a^{2} =a_{c} \cdot c,\ b^{2} =b_{c} \cdot c$
Высота, опущенная из вершины прямого угла на гипотенузу, делит гипотенузу в таком отношении, в каком находятся квадраты прилежащих катетов:
$\frac{a_{c}}{b_{c}} =\frac{a^{2}}{b^{2}}$

Примеры решения задач

ПРИМЕР 1

Задание

В прямоугольном треугольнике $ABC$ гипотенуза $BC=20$ см. Найти длину высоты $AH$ , если $HC=15$ см.

Решение

Найдем длину отрезка 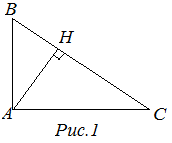$BH$ :

Пример 1, пропорциональные отрезки в прямоугольном треугольнике

$BH=BC-HC=20-15=5$ см.

Поскольку $BH$ и $HC$ – проекции катетов $AB$ и $AC$ на гипотенузу, то можно записать следующее равенство:

$AH^{2} =BH \cdot HC=5\cdot 15=75,$

откуда

$AH=\sqrt{75} =5\sqrt{3} cm$

Ответ

$AH=5\sqrt{3}$ см

ПРИМЕР 2

Задание

В прямоугольном треугольнике высота, опущенная из вершины прямого угла, делит гипотенузу на отрезки $36$ см и $64$ см. Найти все стороны треугольника.

Решение

Рассмотрим прямоугольный треугольник $ABC$ ( $\angle A=90^{\circ}$ ) (рис.1). Из вершины $A$ опустим высоту $AH$ , которая разделит гипотенузу $BC$ на отрезки $BH=36$ см и $CH=64$ см, которые являются проекциями катетов на гипотенузу. Найдем длину гипотенузы:

$BC=BH+HC=36+64=100\ cm$