Признаки равностороннего треугольника
Определение и признаки равностороннего треугольника
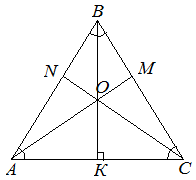
Существует несколько признаков, по которым можно определить, что треугольник является равносторонним.
- В равностороннем треугольнике все углы равны между собой и равны
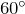 :
: - В равностороннем треугольнике высоты, являются биссектрисами и медианами и пересекаются в одной точке, которая называется центром равностороннего треугольника.
- Центр равностороннего треугольника является центром вписанной и описанной окружностей.
![]()
Для равностороннего треугольника справедливы следующие соотношения:
- В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной.
- В равностороннем треугольнике со стороной
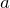 радиус описанной окружности равен
радиус описанной окружности равен 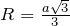 , а радиус вписанной окружности –
, а радиус вписанной окружности – 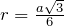 .
. - В равностороннем треугольнике высоты совпадают с медианами и биссектрисами и равны
![Rendered by QuickLaTeX.com \[h=m=l=\frac{a\sqrt{3}}{2} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f45ad5433ba5f7cb42ef3f7dbcd55990_l3.png)
- Площадь равностороннего треугольника со стороной
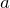 равна
равна
![Rendered by QuickLaTeX.com \[S=\frac{a^{2} \sqrt{3}}{4} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-2fba8d82547dc055a06aa9ca5fa09e04_l3.png)
Примеры решения задач
| Задание | В равностороннем треугольнике 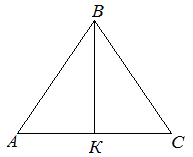
|
| Решение | Так как треугольник Из последнего равенства выразим |
| Ответ |
| Задание | Известно, что радиус окружности, вписанной в равносторонний треугольнике 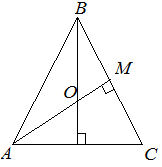
|
| Решение | Радиус окружности, вписанной в равносторонний треугольник, связан со стороной треугольника равенством
А сторона треугольника связана с высотой следующим соотношением: Откуда |
| Ответ |











