Формулы равностороннего треугольника
Определение и формулы равностороннего треугольника
ОПРЕДЕЛЕНИЕ
Треугольник называется равносторонним, если все его стороны равны.
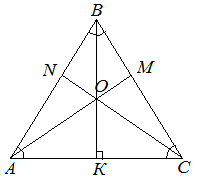
В равностороннем треугольнике все углы равны между собой и равны 
:
![\[\angle A=\angle B=\angle C=60^{\circ} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-53c3bec26ef18686459862aefe17a326_l3.png "Rendered by QuickLaTeX.com")
В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной
![\[R=2r\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f16074bae7df0944cb99cfc0ea98217c_l3.png "Rendered by QuickLaTeX.com")
В равностороннем треугольнике со стороной 
радиус описанной окружности равен 
, радиус вписанной окружности – 
.
В равностороннем треугольнике высоты совпадают с медианами и биссектрисами и равны 
.
Площадь равностороннего треугольника равна 
.
Примеры решения задач
ПРИМЕР 1
| Задание | Найти сторону равностороннего треугольника  , если биссектриса  см.
|
| Решение | Так как треугольник равносторонний, то его биссектриса
Тогда сторона треугольника |
| Ответ |  см
|
![\[BK=\frac{AC\sqrt{3}}{2} =6\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-27ca8f102334fbf53a0770ff670d5d45_l3.png "Rendered by QuickLaTeX.com")
![\[AC=\frac{2\cdot 6}{\sqrt{3}} =4}\sqrt{3}} cm \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e80cae76ac55bca53275e24a3f8af366_l3.png "Rendered by QuickLaTeX.com")
ПРИМЕР 2
| Задание | Найти высоту равностороннего треугольника , если радиус вписанной окружности равен 3 см.
|
| Решение | Зная радиус вписанной окружности в равносторонний треугольник, можно найти его сторону:
Сторона треугольника связана с высотой следующим соотношением |
| Ответ |  см
|
![\[AC=\frac{6\cdot ON}{\sqrt{3}} =6\sqrt{3} cm \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-887c47f51de5d7e6a472f81abbc627d1_l3.png "Rendered by QuickLaTeX.com")
![\[BN=\frac{AC\sqrt{3}}{2} =\frac{6\sqrt{3} \cdot \sqrt{3}}{2} =9 cm \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-c77d8847fcee151d66ff582f832a832b_l3.png "Rendered by QuickLaTeX.com")
