Формулы прямоугольного треугольника

Определение и формулы прямоугольного треугольника

ОПРЕДЕЛЕНИЕ

Если один из углов треугольника прямой (то есть равен ${90}^\circ$ ), то треугольник называется прямоугольным.

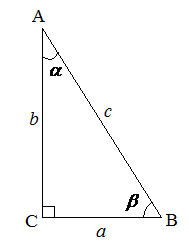
В прямоугольном треугольнике $ABC$ с $\angle C=90^{\circ} ,\ \angle A=\alpha$ , гипотенузой $AB=c$ и катетами $AC=b$ и $BC=a$

$\sin \alpha =\frac{BC}{AB} =\frac{a}{c} ,\ \cos \alpha =\frac{AC}{AB} =\frac{b}{c} ,$

$\text{tg}\alpha =\frac{BC}{AC} =\frac{a}{b} ,\ \text{ctg}\alpha =\frac{AC}{BC} =\frac{b}{a}$

Теорема Пифагора:

$AC^{2} +BC^{2} =AB^{2} \Leftrightarrow a^{2} +b^{2} =c^{2}$

Площадь прямоугольного треугольника:

$S=\frac{1}{2} ab$

Радиус окружности, вписанной в прямоугольный треугольник

$r=\frac{a+b-c}{2}$

Радиус окружности, описанной около прямоугольного треугольника

$R=\frac{c}{2}$

Примеры решения задач

ПРИМЕР 1

Задание

В прямоугольном треугольнике с катетом 6 см и прилежащим к нему острым углом $60^{\circ}$ найти периметр и площадь.

Решение

Рассмотрим прямоугольный треугольник $ABC\ (\angle C=90^{\circ} )$ . Пусть катет $CB=6$ см и $\angle B=60^{\circ}$ . Найдем длину гипотенузы $AB$ :

$AB=\frac{CB}{\cos 60^{\circ}} =\frac{6}{1/2} =12 cm$

Тогда по теореме Пифагора второй катет

$AC=\sqrt{AB^{2} -CB^{2}} =\sqrt{144-36} =\sqrt{108} =6\sqrt{3} cm$

Найдем периметр и площадь треугольника

$P=AC+CB+AB=12+6+6\sqrt{3} =(18+6\sqrt{3} ) cm ,$

$S=\frac{AC\cdot CB}{2} =\frac{6\sqrt{3} \cdot 6}{2} =18\sqrt{3} cm ^{2}$

Ответ

$P=(18+6\sqrt{3} )$ см, $S=18\sqrt{3}$ см $^{2}$

ПРИМЕР 2

Задание

В прямоугольном треугольнике известно, что радиус описанной окружности $R=6,5$ см, а радиус вписанной окружности $r=2$ см. Найти стороны треугольника.