Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Формулы по геометрии Треугольник Стороны равностороннего треугольника

Стороны равностороннего треугольника

Определение и формулы для вычисления сторон равностороннего треугольника

ОПРЕДЕЛЕНИЕ

Треугольник называется равносторонним, если все его стороны равны.

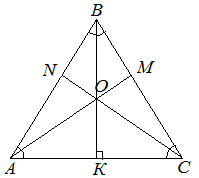
Стороны равностороннего треугольника

Для равностороннего треугольника справедливы следующие утверждения:

В равностороннем треугольнике со стороной 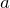$a$ радиус описанной окружности равен 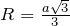$R=\frac{a\sqrt{3}}{3}$ , радиус вписанной окружности – $r=\frac{a\sqrt{3}}{6}$ .
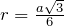В равностороннем треугольнике высоты совпадают с медианами и биссектрисами и выражаются через сторону треугольника по формуле

$h=\frac{a\sqrt{3}}{2}$

Площадь равностороннего треугольника выражается через сторону 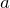$a$ следующим образом:

$S=\frac{a^{2} \sqrt{3}}{4}$

Примеры решения задач

ПРИМЕР 1

Задание

В равностороннем треугольнике 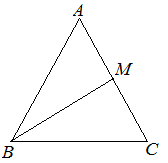$ABC$ известна медиана $BM=10$ см. Найти сторону этого треугольника.

Пример 1, стороны равностороннего треугольника

Решение

Так как треугольник $ABC$ равносторонний, то его медиана является высотой и биссектрисой и выражается через сторону треугольника по формуле

$BM=\frac{AC\sqrt{3}}{2} =10$

Из последнего равенства получаем, что

$AC=\frac{2\cdot 10}{\sqrt{3}} =\frac{20\sqrt{3}}{3} cm$

Ответ

$AC=\frac{20\sqrt{3}}{3}$ см

ПРИМЕР 2

Задание

В равностороннем треугольнике 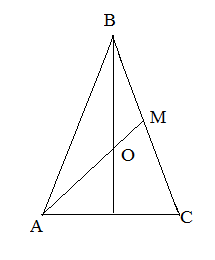$ABC$ радиус вписанной окружности равен $2\sqrt{3}$ см. Найти медиану треугольника.

Пример 3, стороны равностороннего треугольника

Решение

Поскольку радиус вписанной окружности в равностороннем треугольнике равен

$OM=\frac{AC\sqrt{3}}{6} ,$

то

$AC=\frac{6OM}{\sqrt{3}} =\frac{6\cdot 2\sqrt{3}}{\sqrt{3}} =12 cm$

А сторона треугольника связана с медианой следующим соотношением:

$AM=\frac{AC\sqrt{3}}{2} =\frac{12\sqrt{3}}{2} =6\sqrt{3} cm$

Ответ

$AM=6\sqrt{3}$ см

© SolverBook - онлайн сервисы для учебы, 2015

Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.

Почта для связи: info@ru.solverbook.com

Выберите язык:

Сервисы

SolverBook