Формулы равнобедренного треугольника
Определение и формулы равнобедренного треугольника
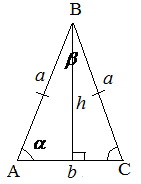
Формулы, выражающие стороны равнобедренного треугольника:
![]()
Площадь равнобедренного треугольника:
![]()
Радиус вписанной окружности
![]()
Радиус описанной окружности
![]()
Примеры решения задач
| Задание | Найти длину боковой стороны равнобедренного треугольника 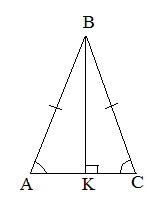
|
| Решение | В треугольнике откуда |
| Ответ |
| Задание | В равнобедренном треугольнике 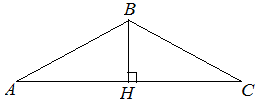
|
| Решение | В равнобедренном треугольнике высота, опущенная на основание, является биссектрисой и медианой, поэтому
а Тогда из прямоугольного треугольника |
| Ответ |











