Площадь равнобедренного треугольника
Площадь равнобедренного треугольника ![]() (рис 1) с боковой стороной
(рис 1) с боковой стороной ![]() и основанием
и основанием ![]() можно вычислить, используя следующие формулы:
можно вычислить, используя следующие формулы:
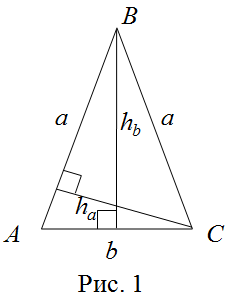
1. Полупроизведение стороны на высоту, проведенную к этой стороне:
 или
или 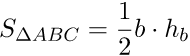
2. Площадь равна квадрату боковой стороны на синус угла при вершине:
![Rendered by QuickLaTeX.com \[ S_{\Delta ABC} = \frac{1}{2} a^{2} \cdot \sin \angle B \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-87ea825e1297153443a303723c9dbda4_l3.png)
3. Так как полупериметр равнобедренного треугольника равен
![]()
то в этом случае формула Герона примет вид:
![Rendered by QuickLaTeX.com \[ S_{\Delta ABC} = \frac{b}{2} \sqrt{\left( a^{2} - \frac{b^{2}}{4} \right) } \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-33bb3dba64deb8de77c9c1eb305b4718_l3.png)
4. Через радиус описанной окружности:
![Rendered by QuickLaTeX.com \[ S_{\Delta ABC} = \frac{a^{2}b}{4R} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9bd8f6327f0e6a18eac319e4f7eb6a84_l3.png)
где ![]() – радиус описанной окружности.
– радиус описанной окружности.
5. Через радиус вписанной окружности и полупериметр:
![Rendered by QuickLaTeX.com \[ S_{\Delta ABC} = \left( a + \frac{b}{2} \right) r \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-612a4df4eae6507968f4b308613c34b6_l3.png)
где ![]() – радиус вписанной окружности.
– радиус вписанной окружности.
Примеры решения задач
| Задание | Найти площадь равнобедренного треугольника, у которого боковая сторона равна |
| Решение | Обозначим боковые стороны заданного треугольника Подставляя исходные данные задачи, получим
|
| Ответ |
| Задание | В равнобедренном треугольнике |
| Решение | Сделаем рисунок (рис. 2).
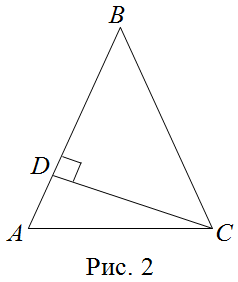
По условию задачи
Из треугольника
Для нахождения площади заданного треугольника воспользуемся формулой которая в нашем случае перепишется в виде Подставляя в последнее равенство значения
|
| Ответ |






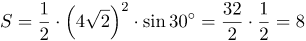 (см
(см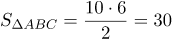 (см
(см




