Стороны равнобедренного треугольника

Определение и формулы для вычисления сторон равнобедренного треугольника

ОПРЕДЕЛЕНИЕ

Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами, а третья – основанием треугольника.

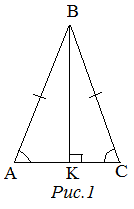
Для равнобедренного треугольника справедливы следующие утверждения

В равнобедренном треугольнике углы при основании равны:

$\angle A=\angle C$

В равнобедренном треугольнике медиана, проведенная к основанию, является одновременно и биссектрисой, и высотой треугольника:

$BK\bot AC,\ AK=KC,\ \angle ABK=\angle CBK$

Примеры решения задач

ПРИМЕР 1

Задание

В равнобедренном треугольнике $ABC$ основание $AC$ на 2 см меньше боковой стороны, высота $BK=5$ см, а площадь равна $50 cm ^{2}$ . Найти длину боковой стороны?

Решение

В треугольнике $ABC$ обозначим основание $AC=x$ , тогда боковые стороны $AB=BC=\left(x+2\right)$ . Найдем площадь треугольника:

$S_{\Delta ABC} =\frac{1}{2} \cdot AC\cdot BK=\frac{1}{2} \cdot x\cdot 5=\frac{5x}{2} =50,$

откуда $x=20$ . Следовательно,

$AB=BC=20+2=22 cm$

Ответ

$AB=BC=22$ см

ПРИМЕР 2

Задание

Найти стороны равнобедренного треугольника, если известно, что медиана, проведенная к основанию равна 4 см, а угол при основании равен $45^{\circ}$ .

Решение

Рассмотрим равнобедренный треугольник $ABC$ (рис. 1). Поскольку медиана, проведенная к основанию равнобедренного треугольника, является высотой, то можно рассмотреть прямоугольный треугольник $ABK$ из которого

$AB=\frac{BK}{\sin \angle A} =\frac{4}{\sin 45^{\circ}} =\frac{4}{\frac{\sqrt{2}}{2}} =\frac{8}{\sqrt{2}} =4\sqrt{2} cm ,$

$AK=BK\cdot \text{ctg}\angle A=4\cdot 1=4cm$

Так как $AC=2AK$ , то $AC=8$ см.

Ответ

$AB=BC=4\sqrt{2}$ см, $AC=8$ см

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Стороны равнобедренного треугольника

Определение и формулы для вычисления сторон равнобедренного треугольника

Примеры решения задач