Закон сохранения заряда

Закон сохранения электрического заряда связан с его релятивистской инвариантностью. Если бы величина заряда зависела от скорости его движения, то при движении зарядов какого-либо знака изменялся бы суммарный заряд изолированной системы.

Формулировки закона сохранения заряда

Совокупный заряд электрически изолированной системы остается постоянным. В математическом виде данное утверждение можно представить как:

$q_1+q_2+\dots +q_n={q'}_1+{q'}_2+\dots +{q'}_n\left(1\right)$

Электрический заряд может исчезать и появляться снова. Но всегда появляются и исчезают два заряда равные по модулю и противоположные по знаку.

Закон сохранения заряда можно пояснить, следуя двум положениям:

Электрон и протон являются материальными частицами с бесконечным временем жизни, инвариантными зарядами, не зависящими от скорости их перемещения.
2Помимо электронов и протонов имеются другие элементарные частицы, которые принимают участие в процессах взаимных превращений, но какие превращения не происходят, суммарный заряд частиц во всех процессах не изменяется.

В приведенной трактовке закон сохранения заряда — это следствие неуничтожимости носителей заряда. Следует заметить, что заряд не может существовать отдельно от материи, которая является его носителем.

Несколько иная формулировка закона сохранения заряда может быть следующей:

Изменение заряда в некотором объеме (V) может происходить исключительно как следствие втекания или вытекания заряда через замкнутую поверхность (S), ограничивающую рассматриваемый объем. Такая формулировка закона позволяет математически записать закон сохранения заряда в виде:

$\frac{\partial }{\partial t}\int_V{\rho dV}=-\oint_S{\overline{j}\cdot d\overline{S}\left(2\right),}$

где $\overline{j}\cdot d\overline{S}=jdScos(\widehat{\overline{j}\cdot d\overline{S}})$ , $\overline{j}$ — плотность тока; $\frac{\partial }{\partial t}\int_V{\rho dV}$ — скорость изменения заряда в заданном объеме. Знак минус в выражении (2) показывает то, что если положительный заряд внутри объема уменьшатся, то плотность тока направлена из объема V. Вектор $d\overline{S}$ имеет направление вдоль внешней нормали к поверхности S. Выражение (2) называют интегральным.

Закон сохранения заряда можно записать и в локальной форме:

$\frac{\partial \rho }{\partial t}+div\overline{j}=0\ \left(3\right)$

где $div\overline{j}=\frac{\partial j_x}{\partial x}+\frac{\partial j_y}{\partial y}+\frac{\partial j_z}{\partial z}.$ Уравнение (3) называют уравнением непрерывности.

Примеры решения задач

ПРИМЕР 1

Задание

Два одинаковых металлических шарика имеют заряды $2q$ и $-5q$ . Их привели в соприкосновение. Какими станут заряды шариков?

Решение

Основой для решения задачи служит закон сохранения заряда, который мы запишем в виде:

$q_1+q_2+\dots +q_n={q'}_1+{q'}_2+\dots +{q'}_n\left(1.1\right)$

Для нашего случая он преобразуется к виду:

$q_1+q_2={q'}_1+{q'}_2\left(1.2\right)$

Так как шарики одинаковые, то можно записать, что:

${q'}_1={q^'}_2=q'(1.3)$

Соответственно, выражение (1.2) можно записать как:

$q_1+q_2=2q'\to q'=\frac{q_1+q_2}{2}$

Не забывая, что должны учесть знаки зарядов, получаем:

$q'=\frac{2q-5q}{2}=-1,5q$

Ответ

$q'=-1,5q$

ПРИМЕР 2

Задание

Два одинаковых проводящих шарика подвешены на нитях (длины нитей одинаковы). Поверхности шариков соприкасаются (рис.1). Какой заряд следует сообщить шарикам для того, чтобы сила натяжения нитей стала равной N? Считайте, что масса одного шарика равна 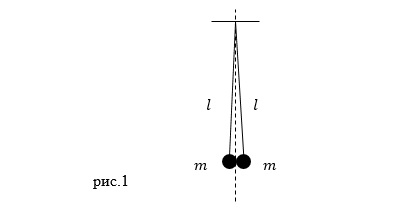$m$ , расстояние от центра шарика до точки подвеса равно $l$ .

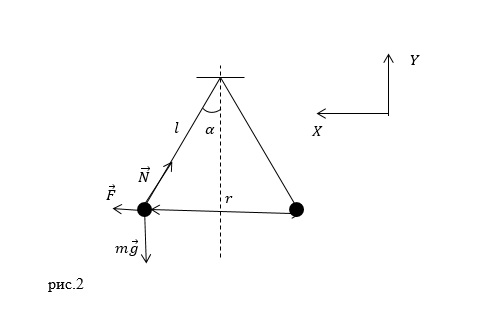
Решение

После того, как шарикам сообщают заряды, они отталкиваются друг от друга (возникает сила Кулона ( $\overline{F}$ )) и подвес отклоняется не некоторый угол $\alpha$ (от вертикали). После этого шарики приходят в равновесие.

По закону сохранения заряда, если одинаковым шарикам сообщают заряд q, то можно записать:

$q=q_1+q_2\left(2.1\right)$

Но так как по условию шарики одинаковые, то $q_1=q_2$ выражение (2.1) преобразуется к виду:

$q={2q}_1\to q_1=\frac{q}{2}\left(2.2\right)$

Условия равновесия обоих шариков для нашей задачи одинаковы, то будем рассматривать только один шарик. Рассмотрим силы, приложенные к шарику, и запишем второй закон Ньютона:

$m\overline{g}+\overline{N}+\overline{F}=0\left(2.3\right)$

Запишем проекции уравнения (2.3) на оси X и Y:

$X:F-Nsin\left(\alpha \right)=0\to F=Nsin\left(\alpha \right)\left(2.4\right)$

$Y:Ncos\left(\alpha \right)-mg=0\to cos\left(\alpha \right)=\frac{mg}{N}\to sin\left(\alpha \right)=\sqrt{1-{\left(\frac{mg}{N}\right)}^2}\left(2.5\right)$

Модуль силы Кулона можно найти по закону Кулона, приняв шарики за точечные:

$F=\frac{1}{4\pi {\varepsilon }_0}\frac{{q_1}^2}{r^2}\left(2.6\right),$

где расстояние между шариками можно найти как (рис.2):

$r=2lsin\left(\alpha \right)\left(2.6\right)$

Тогда выражение для силы Кулона примет вид (примем $\varepsilon =1$ ):

$F=\frac{1}{4\pi {\varepsilon }_0}\frac{{q_1}^2}{{4l}^2{sin}^2\left(\alpha \right)}\left(2.7\right)$

Учитывая выражения (2.7), (2.4) и (2.5) запишем:

$\frac{1}{4\pi {\varepsilon }_0}\frac{{q_1}^2}{{4l}^2\left(1-{\left(\frac{mg}{N}\right)}^2\right)}=N\sqrt{1-{\left(\frac{mg}{N}\right)}^2}\to q_1=4l\sqrt{\pi N{\varepsilon }_0{\left(1-{\left(\frac{mg}{N}\right)}^2\right)}^{\frac{3}{2}}}$

Значит, помня (2.2), получим:

${q=2q}_1=8l\sqrt{\pi N{\varepsilon }_0{\left(1-{\left(\frac{mg}{N}\right)}^2\right)}^{\frac{3}{2}}}$

Ответ

$q=8l\sqrt{\pi N{\varepsilon }_0{\left(1-{\left(\frac{mg}{N}\right)}^2\right)}^{\frac{3}{2}}}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Закон сохранения заряда

Формулировки закона сохранения заряда

Примеры решения задач