Формула электрического заряда

Определение и формула электрического заряда

ОПРЕДЕЛЕНИЕ

Электрический заряд – это первичное понятие, что означает, его нельзя определить при помощи других еще более простых понятий, можно только описать его свойства. Электрический заряд определяет способность тел к электрическому взаимодействию.

Фундаментальным свойством электрического заряда является существование двух видов зарядов: положительных и отрицательных. Заряды, имеющие один знак, отталкиваются. Взаимодействие зарядов разного знака определяют как притяжение. Телу можно сообщить заряд любого знака. В макроскопическом теле заряды разных знаков могут взаимно компенсировать друг друга.

Электрический заряд является релятивистски инвариантной величиной. Это значит, что величина заряда не зависит от системы отсчета, не важно, движется заряд (заряженное тело) или покоится.

Электрический заряд тела находят как суммарный заряд его частей.

Разделения электрических зарядов разных знаков можно добиться путем электризации посредством непосредственного контакта тел (например, трением) или без контакта, например посредством электрической индукции. При зарядке тела, мы создаем на нем избыток электронов или недостаток в сравнении с их нормальным количеством, при котором тело не имеет заряда. При этом электроны берутся у другого тела или удаляются из заряжаемого тела, но не уничтожаются или создаются. Важно запомнить, что процесс зарядки и разрядки тел является процедурой перераспределения электронов, при этом общее их число не изменяется.

При соединении заряженного проводника с незаряженным, заряд перераспределяется между обоими телами. Допустим, что одно тело несет отрицательный заряд, его соединяют с незаряженным телом. Электроны заряженного тела под воздействием сил взаимного отталкивания переходят на незаряженное тело. При этом заряд первого тела уменьшается, заряд второго увеличивается, до тех пор, пока не наступит равновесие.

Элементарный заряд

Немецкий физик и физиолог Г. Гельмгольц обратил внимание на то, что заряды, которые переносят ионы при явлении электролиза, являются целыми, кратными некоторой величине, равной $q=1,6\cdot {10}^{-19}$ Кл. Каждый одновалентный ион переносит такой заряд. Любой двухвалентный ион несет заряд, равный $2\cdot 1,6\cdot {10}^{-19}$ Кл, и так далее. Гельмгольц сделал вывод о том, что заряд $q=1,6\cdot {10}^{-19}$ Кл является минимальным количеством электричества, которое существует в природе. Данный заряд получил название элементарного заряда.

Закон сохранения заряда

Закон сохранения заряда является фундаментальным законом природы. Он был установлен на основании обобщения экспериментальных данных. Подтвержден в 1843 г. английским физиком М. Фарадеем.

Формулировка закона: В любой замкнутой системе алгебраическая сумма зарядов – это неизменная величина, и не важно, какие процессы происходят в этой системе:

$\sum^N_{i=1}{q_i}=const\ \qquad(1)$

где N – количество зарядов.

Закон Кулона

На вопрос: С какими силами взаимодействуют неподвижные точечные заряды? Отвечает закон Кулона, который можно записать в виде формулы как:

$\overline{F}=\frac{q_1q_2}{4\pi \varepsilon {\varepsilon }_0r^3_{12}}{\overline{r}}_{12} \qquad(2)$

где $\overline{F}$ – сила, с которой заряд $q_2$ действует на заряд $q_1$ ; ${\overline{r}}_{12}$ – радиус вектор, который проведен от второго заряда к первому; ${\varepsilon }_0=8,85\cdot {10}^{-12}\frac{\Phi}{m}$ – электрическая постоянная; $\varepsilon$ – диэлектрическая проницаемость вещества в котором находятся заряды. В соответствии с третьим законом Ньютона первый заряд действует на второй с силой равной по модулю и противоположной по направлению силе $\overline{F}.$ Обратите внимание, что заряды в формуле (2) точечные.

Примеры решения задач по теме «Электрический заряд»

ПРИМЕР 1

Задание

Два одинаковых проводящих шарика находятся на расстоянии, которое много больше, чем размеры самих шариков. Шарики несут заряды разного знака, причем заряд одного из них по модулю в два раза больше, чем другого. Шарики соединили и снова разнесли на прежнее расстояние. Найдите отношение ( $\frac{F_1}{F_2}$ ) силы взаимодействия шариков до соединения ( $F_1$ ) к силе их взаимодействия поле соединения ( $F_2$ ).

Решение

До соединения система из двух шариков имела заряд:

$-q+2q=q\ \qquad(1.1)$

По условию шарики имеют заряды разных знаков. При их соединении суммарный заряд шариков (q) распределяется поровну между шарами, так как шарики одинаковы. Какие бы манипуляции мы не производили с шариками, если система замкнута, то суммарный заряд не изменится. После соединения каждый шарик имеет заряд равный:

$\frac{q}{2} \qquad(1.2)$

В первом случае сила Кулона по модулю будет равна:

$F_1=\frac{q_1q_2}{4\pi \varepsilon {\varepsilon }_0r^2}=\frac{q\cdot 2q}{4\pi \varepsilon {\varepsilon }_0r^2} \qquad(1.4)$

Во втором случае имеем:

$F_2=\frac{q_1'q_2'}{4\pi \varepsilon {\varepsilon }_0r^2}=\frac{\frac{q}{2}\cdot \frac{q}{2}}{4\pi \varepsilon {\varepsilon }_0r^2}=\frac{q^2}{16\pi \varepsilon {\varepsilon }_0r^2} \qquad(1.4)$

Найдем отношение $\frac{F_1}{F_2}$ :

$\frac{F_1}{F_2}=\frac{q\cdot 2q}{4\pi \varepsilon \varepsilon _0r^2}\cdot \frac{16\pi \varepsilon {\varepsilon }_0r^2}{q^2}=8$

Ответ

$\frac{F_1}{F_2}=8$

ПРИМЕР 2

Задание

Какова сила взаимодействия тонкого, длинного равномерно заряженного стержня и точечного заряда Q, расположение которых показано на рис.1? Длина стержня l, плотность распределения заряда по стержню равна 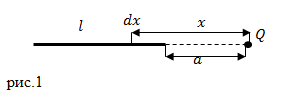$\tau$ , расстояние от ближайшего конца стержня до заряда Q равно a.

Решение

Выделим на стержне элемент ( $dq$ ), который можно считать точечным зарядом (рис.1) на расстоянии x от заряда Q. Силу Кулона ( $dF$ ) для зарядов $dq$ и Q найдем как:

$dF=\frac{dqQ}{4\pi \varepsilon {\varepsilon }_0x^2} \qquad(2.1)$

Если брать следующий элементарный заряд на стержне, то сила его взаимодействия с зарядом Q будет направлена, как и сила $dF$ , следовательно, результирующую силу взаимодействия стержня и точечного заряда можно найти как:

$F=\int{dF}=\int^{a+l}_a{\frac{dqQ}{4\pi \varepsilon {\varepsilon }_0x^2}=}\int^{a+l}_a{\frac{dx}{x^2}=-}\frac{\tau Q}{4\pi \varepsilon {\varepsilon }_0}({\left.\frac{1}{x})\right|}^{a+l}_a=\frac{\tau Ql}{4\pi \varepsilon {\varepsilon }_0a\left(a+l\right)}$

где мы учли, что $dq=\tau dx$ .