Теорема о трех перпендикулярах
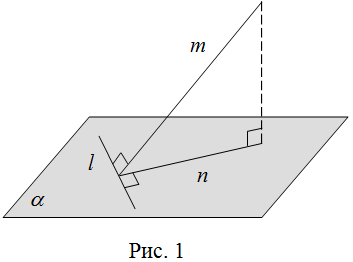
Доказательство теоремы о трех перпендикулярах
Рассмотрим плоскость ![]() . Прямая
. Прямая ![]() перпендикулярна к этой плоскости, так как она перпендикулярна к двум пересекающимся прямым
перпендикулярна к этой плоскости, так как она перпендикулярна к двум пересекающимся прямым ![]() и
и ![]() , лежащим в плоскости
, лежащим в плоскости ![]() по условию и
по условию и ![]() , так как
, так как ![]() . Отсюда следует, что прямая
. Отсюда следует, что прямая ![]() перпендикулярна к любой прямой, лежащей в плоскости
перпендикулярна к любой прямой, лежащей в плоскости ![]() , в частности
, в частности ![]() .
.
Теорема доказана.
Примеры решения задач
| Задание | В треугольнике |
| Решение | Сделаем рисунок (рис. 2).
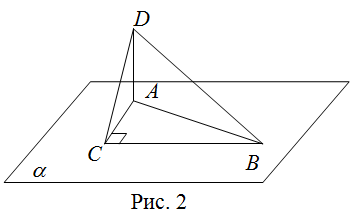
Пусть треугольник По условию, так как в Что и требовалось доказать. |
| Задание | Из вершины |
| Решение | Сделаем рисунок (рис. 3).
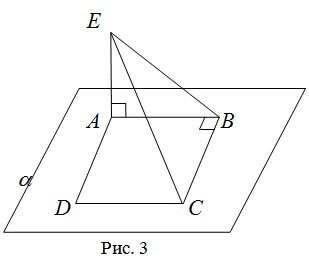
Обозначим Площадь прямоугольного треугольника По условию
Формула для нахождения площади Подставляя в это равенство заданное значение
|
| Ответ |






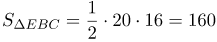 (см
(см




