Теорема Менелая
![Rendered by QuickLaTeX.com \[ \frac{AD}{DB} \cdot \frac{BE}{EC} \cdot \frac{CF}{FA} =1 \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-011ad6e76321538f04c54570426fb27b_l3.png)
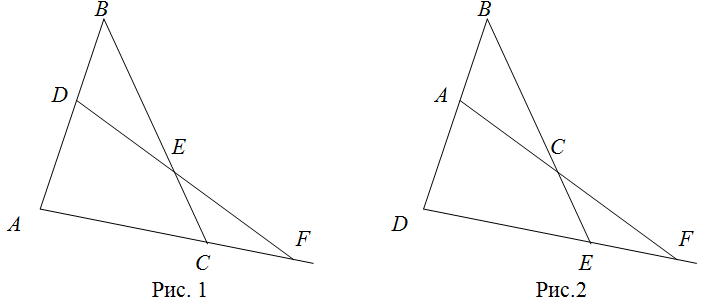
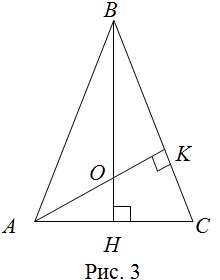
Обратная теорема Менелая
![]()
Примеры решения задач
| Задание | Задан |
| Решение | Обозначим Проверим выполнение этого равенства для нашего треугольника. Подставляем в него введенные обозначения Сокращая дроби в левой части последнего равенства, приходим к очевидному равенству Что и требовалось доказать. |
| Задание | В равнобедренном треугольнике |
| Решение | Сделаем рисунок (рис. 3).
Для площади Подставляя в это равенство заданные значения
Далее, рассмотри прямоугольный треугольник Подставляя значения
После этого применим к Так как |
| Ответ |






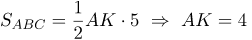 (см)
(см)




