Площадь разностороннего треугольника
Площадь разностороннего треугольника можно вычислить разными способами в зависимости от исходных данных:
Все формулы площади разностороннего треугольника
1. По высоте и основанию
![]()
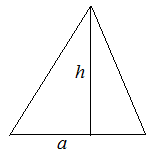
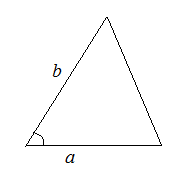
2. По двум сторонам и углу между ними
![]()
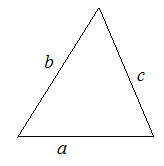
3. По формуле Герона
![]()
где ![]() – полупериметр треугольника
– полупериметр треугольника
4. Через радиусы вписанной и описанной окружностей
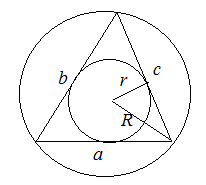
![]()
где ![]() – полупериметр треугольника,
– полупериметр треугольника, ![]() – радиус вписанной окружности;
– радиус вписанной окружности;
![]()
![]() – радиус описанной окружности.
– радиус описанной окружности.
Примеры решения задач
| Задание | Найти площадь треугольника |
| Решение | Запишем для треугольника В первое равенство подставим известные из условия задачи данные: или откуда Тогда искомая площадь |
| Ответ |
| Задание | В треугольнике 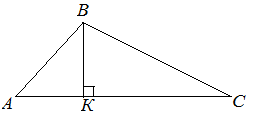
|
| Решение | В треугольнике а из прямоугольного треугольника Тогда сторона а площадь треугольника |
| Ответ |











