Формула электроемкости конденсатора
Проводники у конденсатора называют обкладками конденсатора.
Обкладки должны иметь такую форму и быть расположены так относительно друг друга, что поле, которое создается данной системой, было максимально сосредоточено в ограниченной области пространства, между обкладками.
Назначение конденсатора в том, чтобы накапливать и отдавать в электрической цепи заряд.
Основной характеристикой конденсатора является электрическая емкость (C). Электрическая емкость конденсатора – это взаимная емкость принадлежащих ему обкладок:
![]()
q – величина заряда на обкладке; ![]() – разность потенциалов между обкладками.
– разность потенциалов между обкладками.
Электрическая ёмкость конденсатора зависит от диэлектрической проницаемости диэлектрика, который заполняет пространство между его обкладками. Если пространство между обкладками одного конденсатора заполнено диэлектриком с проницаемостью равной ![]() , а у второго конденсатора воздух между пластинами, то емкость конденсатора с диэлектриком (C) в
, а у второго конденсатора воздух между пластинами, то емкость конденсатора с диэлектриком (C) в ![]() раз больше, чем емкость воздушного конденсатора (
раз больше, чем емкость воздушного конденсатора (![]() ):
):
![]()
Формула электроемкости основных типов конденсаторов
При расчете электроемкости плоского конденсатора нарушением однородности поля около краёв обкладок обычно пренебрегают. Это становится возможным, если расстояние между пластинами существенно меньше, чем линейные размеры обкладок. В таком случае электрическую емкость плоского конденсатора вычисляют при помощи формулы:
![]()
где ![]() – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.
– электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.
Если плоский конденсатор между обкладками имеет N слоев диэлектрика, при этом толщина каждого слоя равна ![]() , а диэлектрическая проницаемость
, а диэлектрическая проницаемость ![]() , то его электрическую емкость рассчитывают при помощи формулы:
, то его электрическую емкость рассчитывают при помощи формулы:
![]()
Цилиндрический конденсатор составляют две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполнено диэлектриком. При этом емкость цилиндрического конденсатора находят как:
![Rendered by QuickLaTeX.com \[C=\frac{2\pi \varepsilon {\varepsilon }_0l}{ln\left(\frac{R_2}{R_1}\right)} \qquad(5)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-36266d632c0c55c5e2ab984c62939edd_l3.png)
где l – высота цилиндров; ![]() – радиус внешней обкладки;
– радиус внешней обкладки; ![]() – радиус внутренней обкладки.
– радиус внутренней обкладки.
У сферического конденсатора обкладками служат две концентрические сферические проводящие поверхности, пространство обкладками заполняет диэлектрик. Емкость сферического конденсатора вычисляют как:
![]()
где ![]() – радиусы обкладок конденсатора. Если
– радиусы обкладок конденсатора. Если ![]() , то можно считать, что
, то можно считать, что ![]() , тогда, мы имеем:
, тогда, мы имеем:
![]()
так как ![]() – площадь поверхности сферы, и если обозначить
– площадь поверхности сферы, и если обозначить ![]() , то получим формулу для емкости плоского конденсатора (3). Если расстояние между обкладками сферического и цилиндрического конденсаторов малы (в сравнении с их радиусами), то в приближенных расчетах используют формулу емкости для плоского конденсатора.
, то получим формулу для емкости плоского конденсатора (3). Если расстояние между обкладками сферического и цилиндрического конденсаторов малы (в сравнении с их радиусами), то в приближенных расчетах используют формулу емкости для плоского конденсатора.
Электрическую емкость для линии из двух проводов находят как:
![]()
где d – расстояние между осями проводов; R – радиус проводов; l – длина линии.
Формулы для вычисления электрической емкости соединений конденсаторов
Если конденсаторы соединены параллельно, то суммарная емкость батареи (C) находится как сумма емкостей отдельных конденсаторов (![]() ):
):
![]()
При последовательном соединении конденсаторов емкость батареи вычисляют как:
![Rendered by QuickLaTeX.com \[\frac{1}{C}=\sum^N_{i=1}{\frac{1}{C_i}}\left(10\right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-58e5ef39e6afde200e05803ccb4d2b2b_l3.png)
Если последовательно соединены N конденсаторов, с емкостями ![]() то емкость батареи найдем как:
то емкость батареи найдем как:
![]()
Сопротивление конденсатора
Если конденсатор включен в цепь с постоянного тока, то сопротивление конденсатора можно считать бесконечно большим.
При включении конденсатора в цепь переменного тока, его сопротивление носит название емкостного, и вычисляют его с помощью формулы:
![]()
где ![]() – частота переменного тока;
– частота переменного тока; ![]() – угловая частота тока; C – емкость конденсатора.
– угловая частота тока; C – емкость конденсатора.
Энергия поля конденсатора
Электрическое поле локализованное между пластинами конденсатора обладает энергией, которую можно вычислить при помощи формулы:
![]()
где ![]() –энергия поля конденсатора; q – заряд конденсатора; C – емкость конденсатора;
–энергия поля конденсатора; q – заряд конденсатора; C – емкость конденсатора; ![]() – разность потенциалов между обкладками конденсатора.
– разность потенциалов между обкладками конденсатора.
Энергия поля плоского конденсатора:
![]()
Примеры решения задач по теме «Электроемкость конденсатора»
| Задание | Воздушный конденсатор обладает энергией электрического поля равной |
| Решение | В качестве основы для решения задачи используем формулу для вычисления энергии поля конденсатора:
Для воздушного конденсатора энергия поля равна: Для конденсатора с диэлектриком: Записывая выражения (1.2) и (1.3) мы учли закон сохранения заряда на конденсаторе, так как при заполнении его диэлектриком конденсатор от источника напряжения отключен. Кроме того, можно записать, что: Выразим емкость Найдем искомое изменение энергии: Проведем вычисления: |
| Ответ | |
| Задание | Изобразите схему соединения конденсаторов с емкостями: |
| Решение | Для решения задачи следует вспомнить формулы для вычисления емкостей соединений конденсаторов. При параллельном соединении конденсаторов емкость батареи (C) равна сумме емкостей отдельных конденсаторов ( При последовательном соединении конденсаторов емкость батареи вычисляют как: В нашей задаче речь идет о смешанном соединении, так как если бы все конденсаторы соединены были параллельно, то емкость батареи была бы равна: Если все наши конденсаторы соединить последовательно, то: Рассмотрим соединение (рис.1): 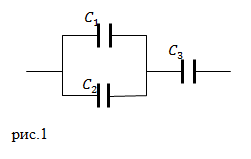
Емкость параллельного соединения конденсаторов равна ( Емкость последовательного соединения |
| Ответ | Требуемая емкость получается при соединении конденсаторов как изображено на рис.1 |






![Rendered by QuickLaTeX.com \[\frac{1}{C}=\sum^N_{i=1}{\frac{1}{C_i}} \qquad(2.1)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-110774ecf798066c3c9cca3dafad67c9_l3.png)





