Емкость конденсатора
![]()
Емкость в Международной системе единиц (СИ) измеряется в фарадах (Ф). Фарад – это большая емкость, поэтому на практике часто применяют пико фарады (пФ), нано фарады (нФ), микро фарады (мкФ).
![]()
Емкость плоского конденсатора
Получим формулу для расчета ёмкости плоского конденсатора, который состоит из двух параллельных проводящих пластин, площадь которых равна S (каждая). Пластины расположены на расстоянии d друг от друга. Одна пластина имеет заряд ![]() а другая
а другая ![]() . Будем считать, что расстояние между пластинами конденсатора много меньше, чем их линейные размеры. В таком случае краевые эффекты можно не принимать в расчет и электрическое поле между обкладками будем считать однородным. Поле (E), которое создают две бесконечные плоскости, несущие одинаковый по модулю и противоположный по знаку заряд, разделенные диэлектриком с диэлектрической проницаемостью
. Будем считать, что расстояние между пластинами конденсатора много меньше, чем их линейные размеры. В таком случае краевые эффекты можно не принимать в расчет и электрическое поле между обкладками будем считать однородным. Поле (E), которое создают две бесконечные плоскости, несущие одинаковый по модулю и противоположный по знаку заряд, разделенные диэлектриком с диэлектрической проницаемостью ![]() , можно определить при помощи формулы:
, можно определить при помощи формулы:
![]()
где ![]() — плотность распределения заряда по поверхности пластины. В таком случае, разность потенциалов между рассматриваемыми обкладками конденсатора, находящимися на расстоянии d будет равна:
— плотность распределения заряда по поверхности пластины. В таком случае, разность потенциалов между рассматриваемыми обкладками конденсатора, находящимися на расстоянии d будет равна:
![]()
Подставим правую часть выражения (3) вместо разности потенциалов в (1) и учитывая, что ![]() , получаем:
, получаем:
![]()
Емкости цилиндрического и сферического конденсаторов получают по аналогичной схеме.
Емкости цилиндрического и сферического конденсаторов
Цилиндрическим называют конденсатор, который представляет собой две соосные цилиндрические поверхности из проводника, разного радиуса, пространство между которыми заполнено диэлектриком. Емкость такого конденсатора находят как:
![Rendered by QuickLaTeX.com \[C=\frac{2\pi \varepsilon {\varepsilon}_0l}{ln\left(\frac{R_2}{R_1}\right)} \qquad (5), \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e6fc4033ecca7b27a841262b55c62975_l3.png)
где l – высота цилиндров; ![]() – радиус внешнего цилиндра;
– радиус внешнего цилиндра; ![]() – радиус внутреннего цилиндра. По формуле (5) вычисляют емкость коаксиального кабеля.
– радиус внутреннего цилиндра. По формуле (5) вычисляют емкость коаксиального кабеля.
Сферическим конденсатором является конденсатор, обкладки которого две концентрические сферические поверхности из проводника, пространство между ними заполняет диэлектрик. Емкость сферического конденсатора определяют как:
![]()
где ![]() – радиусы обкладок конденсатора.
– радиусы обкладок конденсатора.
Примеры решения задач
| Задание | Емкость первого конденсатора составляет 100 пФ, второго — |
| Решение | В качестве основы для решения задачи используем формулу:
Тогда заряд на первом конденсаторе ( На втором конденсаторе заряд равен: По условию конденсаторы подключали к одному источнику постоянного напряжения, поэтому Переведем 100 пФ в фарады: Можно проводить вычисления: |
| Ответ |
| Задание | Проводящий шар помещен в масло ( |
| Решение | Сделаем рисунок.
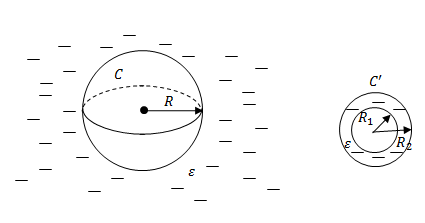
Рис. 1 Емкость уединенного проводящего шара, погруженного в диэлектрик, вычисляется при помощи формулы: Емкость сферического конденсатора найдем как: По условию задачи: Приравняем правые части выражений (2.1) и (2.2), получим: Проведем вычисления радиуса проводящего шара: |
| Ответ |











