Формула емкости конденсатора

ОПРЕДЕЛЕНИЕ

Емкость – один из основных параметров характеризующих конденсатор.

Если q – величина заряда одной из обкладок конденсатора, а $U={\varphi }_1-{\varphi }_2$ – разность потенциалов между его обкладками, то величина C, равная:

$C=\frac{q}{U}=\frac{q}{{\varphi }_1-{\varphi }_2} \qquad(1)$

называется емкостью конденсатора. Это постоянная величина, которая зависит то размеров и устройства конденсатора.

Рассмотрим два одинаковых конденсатора, разница между которым заключается только в том, что между обкладками одного вакуум (или часто говорят воздух), между обкладками другого находится диэлектрик. В таком случае при равных зарядах на конденсаторах разность потенциалов воздушного конденсатора будет в $\varepsilon$ раз меньше, чем между обкладками второго. Значит емкость конденсатора с диэлектриком (C) в $\varepsilon$ раз больше, чем воздушного ( $C_0$ ):

$C=\varepsilon C_0 \qquad(2)$

где $\varepsilon$ – диэлектрическая проницаемость диэлектрика.

За единицу емкости конденсатора принимают емкость такого конденсатора, который единичным зарядом (1 Кл) заряжается до разности потенциалов, равной одному вольту (в СИ). Единицей емкости конденсатора (как и любой эклектической емкости) в международной системе единиц (СИ) служит фарад (Ф).

Формула электрической емкости плоского конденсатора

Поле между обкладками плоского конденсатора обычно считают однородным. Его однородность нарушается только около краев. При вычислении емкости плоского конденсатора этими краевыми эффектами часто пренебрегают. Это следует делать, если расстояние между пластинами мало в сравнении с их линейными размерами. Для расчета емкости плоского конденсатора применяют формулу:

$C=\frac{\varepsilon {\varepsilon }_0S}{d} \qquad(3)$

где ${\varepsilon }_0$ – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.

Электрическая емкость плоского конденсатора, который содержит N слоев диэлектрика толщина каждого $d_i$ , соответствующая диэлектрическая проницаемость i-го слоя ${\varepsilon }_i$ , равна:

$C=\frac{{\varepsilon }_0S}{\sum^N_{i=1}{\frac{d_i}{{\varepsilon }_i}}} \qquad(4)$

Формула электрической емкости цилиндрического конденсатора

Цилиндрический конденсатор представляется собой две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик. Электрическая емкость цилиндрического конденсатора вычисляется как:

$C=\frac{2\pi \varepsilon {\varepsilon }_0l}{ln\left(\frac{R_2}{R_1}\right)} \qquad(5)$

где l – высота цилиндров; $R_2$ – радиус внешней обкладки; $R_1$ – радиус внутренней обкладки.

Формула электрической емкости сферического конденсатора

Сферическим конденсатором называют конденсатор, обкладками которого являются две концентрические сферические проводящие поверхности, пространство между ними заполнено диэлектриком. Емкость такого конденсатора находят как:

$C=\frac{4\pi \varepsilon {\varepsilon }_0R_1R_2}{R_2-R_1} \qquad(6)$

где $R_1{;R}_2$ – радиусы обкладок конденсатора.

Примеры решения задач по теме «Емкость конденсатора»

ПРИМЕР 1

Задание

Какова электрическая емкость плоского двуслойного конденсатора? Один из слоев диэлектрика – фарфор с толщиной $d_1$ =2мм; второй слой – эбонит ( $d_2=1,5$ мм). Площадь пластин конденсатора равна 0,01 м².

Решение

Для решения этой задачи проще всего применить формулу для расчета емкости слоистого плоского конденсатора, учитывая, что мы имеем всего два слоя:

$C=\frac{{\varepsilon }_0S}{\frac{d_1}{{\varepsilon }_1}+\frac{d_2}{{\varepsilon }_2}} \qquad(1.1)$

Перед тем, как провести расчет электрической емкости, в справочниках найдем диэлектрические проницаемости веществ, которые применены в нашем конденсаторе. Так, фарфор имеет диэлектрическую проницаемость равную ${\varepsilon }_1=5$ ; диэлектрическая проницаемость эбонита равна ${\varepsilon }_2=3.$ Электрическая постоянная равна ${\varepsilon }_0=8,85\cdot {10}^{-12}\frac{\Psi}{m}.$ Толщину слоев диэлектрика переведем в метры. $d_1=2мм=0,002$ м; $d_2=1,5мм=0,0015$ м. Получим:

$C=\frac{8,85\cdot {10}^{-12}\cdot 0,01}{\frac{0,002}{5}+\frac{0,0015}{3}}=9,83\cdot {10}^{-11}\ (F)$

Ответ

$C=9,83\cdot {10}^{-11}$ Ф

ПРИМЕР 2

Задание

Сферический конденсатор состоит из двух концентрических металлических сфер, имеющих радиусы $R_1=0,02$ м и $R_1=0,021$ м. Пространство между этими сферами заполняет парафин. Какова емкость этого конденсатора?

Решение

Сделаем рисунок.

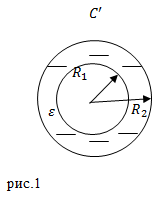
В качестве основы для решения задачи следует применить формулу для вычисления электрической емкости сферического конденсатора:

$C=\frac{4\pi \varepsilon {\varepsilon }_0R_1R_2}{R_2-R_1}$

Прежде чем перейти к вычислениям в справочнике следует найти диэлектрическую проницаемость парафина. Она равна приблизительно двум $\varepsilon \approx 2$ . Найдем величину C:

$C=\frac{4\pi \cdot 2\cdot 8,85\cdot {10}^{-12}\cdot 0,02\cdot 0,021}{0,021-0,02}=46,68\ (pF)$